Упругие деформируемые тела. Внешние и внутренние силы. Напряжения и деформации. Продольные и поперечные деформации. Коэффициент Пуассона. Закон Гука для растяжения, сжатия

Упругие деформируемые тела — это тела, которые после прекращения действия внешних сил, восстанавливают первоначальные размеры и формы.

Внешние силы, действующие на элемент конструкции, подразделяются на 3 группы:

Сосредоточенные силы — силы, действующие на небольших участках поверхности детали (например, давление шарика шарикоподшипника на вал, давление колеса на рельсы и т.п.).

Распределенные силы приложены значительным участкам поверхности (например, давление пара в паропроводе, трубопроводе, котле, давление воздуха на крыло самолета и т.д.).

Объемные или массовые силы приложены каждой частице материала (например, силы тяжести, силы инерции).

Внутри любого материала имеются внутренние межатомные силы. Если к твердому телу приложить внешние силы, то оно будет деформироваться. При этом изменяются расстояния между частицами тела, что в свою очередь приводит к изменению сил взаимного притяжения между ними. Отсюда, как следствие, возникают внутренние усилия. Для определения внутренних усилий используют метод сечения. Для этого тело мысленно рассекают плоскостью и рассматривают равновесие одной из его частей. Метод сечений позволяет выявить внутренние силовые факторы, но для оценки прочности необходимо знать внутренние силы в любой точке сечения. С этой целью введем числовую меру интенсивности внутренних сил – напряжение.

Выделим в сечение площадку размером 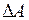. Равнодействующая внутренних сил, действующих на площадку равна , модуль которой зависит от размера выделенной площадки. Равнодействующую разложим на две составляющие: - направленную по нормали к площадке и - действующую по площадке.

Отношение называется средним напряжением по площадке 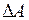. Вектор среднего напряжения совпадает по направлению с вектором равнодействующей .

При уменьшении площадки 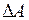изменяются как модуль, так и направление равнодействующей , а вектор приближается к истинному значения значению напряжения в заданной точке.

Числовое значение истинного напряжения выражается равенством

Нормальная сила. При растяжении или сжатие в поперечных сечениях бруса возникает только один внутренний силовой фактор – нормальная сила (рис. 3). Брус имеет два характерных участка. Для определения нормальной силы воспользуемся методом сечения. На расстоянии проведем сечение на первом участке и рассмотрим равновесие отсеченной части (рис. 4). Нормальную силу будем всегда показывать от сечения, что будет соответствовать растяжению бруса.

Составим условие равновесия на ось

Проведем на втором участке сечение на расстоянии . Рассматривая равновесие отсеченной части, получаем . Строим эпюру нормальных сил.

Нормальные напряжения. Исходя из определения напряжения, можно записать

, где нормальное напряжение в произвольной точке сечения.

Согласно гипотезе Бернулли (гипотеза плоских сечений) все продольные волокна бруса деформируются одинаково, а это означает, что напряжения в поперечных сечениях одинаковы, т.е. .

В этом случае получаем , откуда .

Рассчитывая напряжения в каждом сечении, строим эпюру нормальных напряжений.

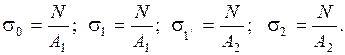
Перемещения и деформации. При растяжении бруса длиной его длина увеличивается на величину , а его диаметр уменьшается на величину (рис.5).

Величина называется абсолютной продольной деформацией, а абсолютной поперечной деформацией.

О степени деформирования бруса нельзя судить по значениям и , так как они зависят не только от действующих сил, но и от

Рис.5

начальных размеров бруса. Для характеристики деформации бруса вводятся понятия относительная продольная деформация и относительная поперечная деформация , которые рассчитываются по зависимостям

отношение называется коэффициентом поперечной деформации или коэффициентом Пуассона.

Для большинства материалов в стадии упругой деформации выполняется соотношение, представляющее собой математическое выражение закона Гука:

где коэффициент пропорциональности, который получил название модуля упругости первого рода.

Подставляя в выражение закона Гука 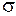и , получим зависимость для определения абсолютного удлинения бруса

откуда

Произведение называется жесткостью бруса при растяжении (сжатии).

Определяя перемещения каждого сечения, строим эпюру продольных перемещений сечений бруса (рис. 3).