Координатный способ задания движения точки

Аналогично для ускорения получаем:
,
где , , - проекции на оси Ox, Oy, Oz. И тогда

(2.6)

5 Оси естественного трехгранника

Построим в точке M кривой линии естественные оси этой кривой (рис. 2.6). Первой естественной осью является касательная . Ее положительное направление в сторону возрастающих расстояний. В другой близкой точке кривой , отстоящей от точки M на расстоянии S, построим касательную ( 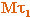и будут скрещиваться). Проведем в точке M прямую , параллельную . Угол между этими линиями называется углом смежности. Кривизной кривой K в точке M называют предел

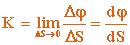
(2.8)

Радиусом кривизны кривой в точке M называют величину, обратную кривизне кривой в этой точке

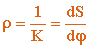
(2.9)

Вычислим, например, радиус кривизны окружности радиусом R (рис. 2.7). Дуга окружности длиной S, опирающаяся на центральный угол φ выражается зависимостью S=Rφ. Для радиуса кривизны имеем:
.
Проведем плоскость через две пересекающиеся прямые и .
Предельное положение этой плоскости при совпадении в пределе точки с точкой M называется соприкасающейся плоскостью кривой в точке M. В случае плоской кривой соприкасающейся плоскостью для всех точек кривой является сама плоскость.

Построим в точке M кривой линии оси естественного трехгранника. Первой осью является касательная (рис. 2.8), или . Перпендикулярно касательной располагается нормальная плоскость кривой. Нормаль, расположенная в соприкасающейся плоскости, называется главной нормалью Mn, или . Она является линией пересечения нормальной плоскости с соприкасающейся плоскостью. По главной нормали внутрь вогнутости кривой направим ось . Она определяет положительное направление второй естественной оси.

Прямая, перпендикулярная главной нормали, называется бинормалью Mb, или . Ось, направленная по бинормали так, чтобы три вектора образовывали правую систему осей координат, определит направление третьей естественной оси . Плоскость, проходящая через , называется спрямляющей.

Три взаимно перпендикулярные оси , , – образуют оси естественного трехгранника. №24

Кривизна кривой

Пусть γ(t) — регулярная кривая в d-мерном евклидовом пространстве, параметризованная длиной. Тогда

называется кривизной кривой γ в точке p = γ(t), здесь обозначает вторую производную по t. Вектор

называется вектором кривизны γ в точке p = γ(t).

Очевидно, это определение можно переписать через вектор касательной:

где одна точка над буквой означает первую производную по t.

Для кривой, заданной параметрически в общем случае (параметр не обязательно является длиной), кривизна отображается формулой

,

где и соответственно обозначают первую и вторую производную радиус-вектора γ в требуемой точке (при этом под крестом для кривой в трехмерном пространстве можно понимать векторное произведение, для кривой в двумерном пространстве — псевдоскалярное произведение, а для кривой в пространстве произвольной размерности — внешнее произведение).

Для того чтобы кривая γ совпадала с некоторым отрезком прямой или со всей прямой, необходимо и достаточно, чтобы кривизна (или вектор кривизны) тождественно равнялась нулю.

Величина, обратная кривизне кривой (r = 1 / κ), называется радиусом кривизны; он совпадает с радиусом соприкасающейся окружности в данной точке кривой. Центр этой окружности называется центром кривизны.

6 Определение ускорения точки

Вектор ускорения a точки лежит в соприкасающейся плоскости P n и определяется двумя проекциями и an (ab = 0):

проекция ускорения точки на касательную равна первой производной от алгебраической скорости или второй производной от криволинейной координаты точки по времени:

= d / dt = d2s /dt2 или = =.

проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой:

an = v2 /.

Величины и an соответственно называют касательным и нормальным ускорениями точки.

Вектор ускорения a является векторной суммой касательной составляющей, напраленной вдоль касательной P, и нормальной составляющей an, направленной вдоль главной нормали Pn:

a = + an.

При этом составляющая может быть направлена или в положительном, или в отрицательном направлении оси P в зависимости от знака проекции, а составляющая an будет всегда направлена в сторону вогнутости кривой, так как проекция an 0.

Так как эти составляющие взаимно перпендикулярны, то модуль вектора a определяется по формуле:

a = (2 + an2)

7 Равнопеременное движение, движение точки, при котором её касательное ускорение wt (в случае прямолинейного Равнопеременное движение всё ускорение w) постоянно. Скорость v, которую имеет точка через t сек после начала движения, и её расстояние s от начального положения, измеренное вдоль дуги траектории, определяются при Равнопеременное движение равенствами:

v = v0 + wt t, s = v0t + wt t2/2,

где v0 — начальная скорость точки. Когда знаки v и wt одинаковы, Равнопеременное движение является ускоренным, а когда разные — замедленным.

Твёрдое тело может совершать поступательное Равнопеременное движение, при котором всё сказанное относится к каждой точке тела, и равнопеременное вращение вокруг неподвижной оси, при котором угловое ускорение тела e постоянно, а угловая скорость w и угол поворота тела j равны: w = w0 + et, j = w0t + et2/2.

8 Скорость и ускорение точки в полярных координатах

Рассмотрим, как вычисляются скорость и ускорение точки при задании ее движения в полярных координатах, то есть когда заданы уравнения движения точки в виде r = r(t); = (t).

В этом случае векторы v и a определяются по их проекциям на взаимно перпендикулярные подвижные оси Pr, имеющие начало в точке Р и движущиеся вместе с нею (см.рис.). Эти оси направлены следующим образом:

ось Pr направлена по радиусу-вектору точки в направлении от полюса О к точки Р;

ось P получается путем поворота вокруг точки Р оси Pr на прямой угол в положительном направлении отсчета угла, то есть против хода часовой стрелки.

Определение скорости точки

Вектор скорости v точки направлен по касательной к траектории и определяется своими проекциями vr и на оси Pr и P по формулам:

vr = dr/dt =;

= r(d /dt) = r.

Величины vr и соответсвенно называются радиальной и трансверсальной скоростями точки.

В зависимости от знаков производных и радиальная и трансверсальная скорости могут быть как положительными, так и отрицательными (на рисунке показан случай, когда обе эти скорости положительные).

Модуль скорости v = (vr2 + 2).

Определение ускорения точки

Вектор ускорения a точки направлен в сторону вогнутости траектории и определяется своими проекциями ar и на оси Pr и P по формулам:

ar = d2r/dt2 - r (d /dt)2 = - r ()2;

= r (d2 /dt2) + 2 (dr/dt) (d /dt) = r + 2.

Величины ar и соответсвенно называются радиальным и трансверсальным ускорениями точки.

Радиальное и трансверсальное ускорения могут быть как положительными, так и отрицательными (на рисунке показан случай, когда радиальное ускорение положительное, а трансверсальное - отрицательное).

Модуль ускорения a = (ar2 + 2).

42 Если два тела I и II (рис. 6.1) взаимодействуют друг с другом, соприкасаясь в точке А, то всегда реакцию RA, действующую, например, со стороны тела II и приложенную к телу I, можно разложить на две составляющие: NA, направленную по общей нормали к поверхности соприкасающихся тел в точке А, и ТА, лежащую в касательной плоскости. Составляющая NA называется нормальной реакцией, сила ТА называется силой трения скольжения — она препятствует скольжению тела I по телу II. В соответствии с аксиомой 4 (третьим законом Ньютона) на тело II со стороны тела I действует равная по модулю и противоположно направленная сила реакции. Ее составляющая, перпендикулярная касательной плоскости, называется силой нормального давления. Сила трения ТА = 0, если соприкасающиеся поверхности идеально гладкие. В реальных условиях поверхности шероховаты и во многих случаях пренебречь силой трения нельзя. Максимальная сила трения приближенно пропорциональна нормальному давлению, т. е. Tmax=fN. (6.3)– закон Амонтона—Кулона. Коэффициент f называется коэффициентом трения скольжения. Его значение не зависит от площади соприкасающихся поверхностей, но зависит от материала и степени шероховатости соприкасающихся поверхностей. Силу трения можно вычислить по ф-ле T=fN только если имеет место критический случай. В других случаях силу трения следует определять из ур-ий равнов. На рисунке показана реакция R (здесь активные силы стремятся сдвинуть тело вправо). Угол j между предельной реакцией R и нормалью к поверхности называется углом трения. tgj=Tmax/N=f.