 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение типовых задач. Пример1. В результате выборки имеем
|
|
Пример1. В результате выборки имеем
-3,+2,-1,-3,+5,-3,+2. Построить график эмпирической функции распределения.
Решение. 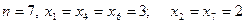 .
.
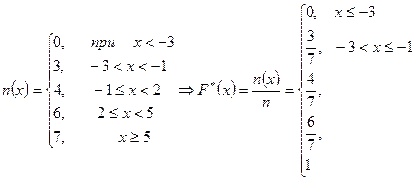
На примере видны основные особенности эмпирической функции распределения. Как и теоретическая, она не убывает, и ее значения 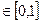 . Но эта формула всегда ступенчатая. Эмпирическая функция не зависит от того, в каком порядке сделана выборка, т.е. от того, в каком порядке идут числа в последовательности:
. Но эта формула всегда ступенчатая. Эмпирическая функция не зависит от того, в каком порядке сделана выборка, т.е. от того, в каком порядке идут числа в последовательности: 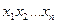 (рис.1).
(рис.1).
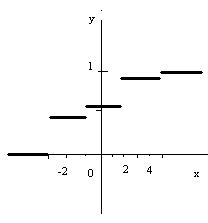
Рисунок 1
Пример 2. Построить гистограмму частот распределения по данной выборке:
Значение 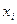
| -2 | ||||||
Частота 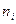
|
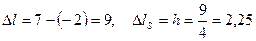 .
.
| Промежуток | [-2;0,25] | [0,25;2,5] | [2,5;4,75] | [4,75;7] |
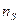
| ||||
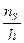
| 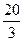
| 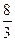
| 
|
По оси ОХ отложим частичные интервалы - вычисленные промежутки, а по оси ОУ значения 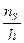 , по которым строим прямоугольники. Совокупность прямоугольников является искомой гистограммой с площадью, равной объему выборки (рис.2).
, по которым строим прямоугольники. Совокупность прямоугольников является искомой гистограммой с площадью, равной объему выборки (рис.2).
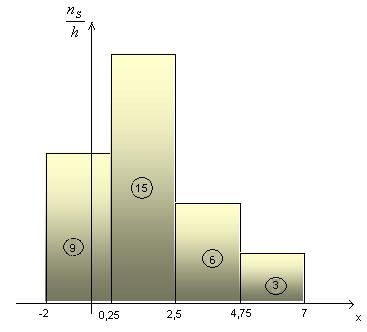
Рисунок 2
Пример3. Контрольные обмеры диаметров болтов дали следующие результаты: 2,31; 2,28; 2,29; 2,28; 2,32; 2,28; 2,32; 2,29; 2,31; 2,32.
Найти точечные оценки для диаметра болта и его дисперсии в контролируемом процессе производства.
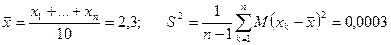 .
.
Пример4. Случайная величина распределена по нормальному закону с параметром 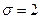 . Сделана выборка
. Сделана выборка 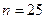 . Найдем с надежностью
. Найдем с надежностью 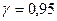 доверительный интервал для неизвестного параметра
доверительный интервал для неизвестного параметра 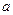 этого распределения.
этого распределения.
Решение.
Из равенства 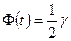 или
или 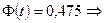 по таблице
по таблице 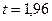 . Тогда точность оценки есть
. Тогда точность оценки есть 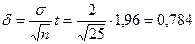 .
.
Тогда 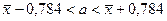 .
.
Если для сделанной выборки 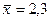 , то с надежностью 0,95 интервал (1,5; 3,1) покрывает параметр
, то с надежностью 0,95 интервал (1,5; 3,1) покрывает параметр 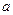 с точностью до 0,8 и надежностью 95 %.
с точностью до 0,8 и надежностью 95 %.
11 ТЕСТОВЫЕ ВОПРОСЫ
Определитель третьего порядка 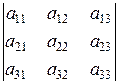 равен:
равен:
A) 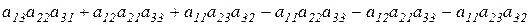
B) 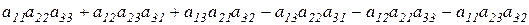
C) 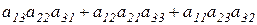
D) 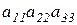
E) 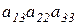
Если в определителе поменять местами две строки, то определитель:
A) уменьшиться в два раза
B) увеличиться в два раза
C) меняется знак
D) не меняется
E) не меняет знак
Если 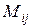 – минор определителя элемента
– минор определителя элемента 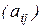 , то алгебраическое дополнение этого элемента равно:
, то алгебраическое дополнение этого элемента равно:
A) 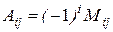
B) 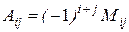
C) 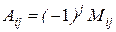
D) 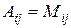
E) 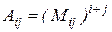
Дата публикования: 2015-11-01; Прочитано: 559 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
