Для вычисления функции Лапласа

.

приведены таблицы для . При , учитываем, что чтобы использовать таблицу формулу (6) переписывают в виде

. (7)

Если число n велико, а число p мало и зависит от номера испытаний, в тоже время величина постоянная, то применяется формула Пуассона.

Теорема Пуассона. Если число , а величина ≠0 постоянная, то

. (8)

9.1.7 Дискретные и непрерывные случайные величины и их числовые характеристики

Определения.

15. Случайной величиной называется величина, которая в результате опыта может принять то или иное (но только одно) значение, причем заранее до опыта неизвестное.

16. Величина, принимающая отдельные изолированные возможные значения, называется дискретной.

Например:

1. а) Х – число нестандартных деталей в партии из 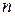штук. Х может принимать значения: .

б) Х – число выстрелов до первого попадания в цель .

2. Биноминальное распределение

3. Распределение Пуассона

4. Геометрическое распределение

5. Гипергеометрическое распределение

17. Непрерывной случайной величиной называется величина, возможные значения которой, заполняют сплошь некоторый интервал.

Например. Х – расстояние, которое пролетит снаряд при выстреле из орудия: .

9.1.8 Закон распределения дискретных случайных величин

Для полного определения случайной величины Х, кроме возможных значений Х, необходимо указать связь между возможными значениями и соответствующими вероятностями. Эта связь называется законом распределения Х и для дискретной случайной величины ее можно задать в виде ряда распределения

			…
			…

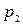
где .

Можно задать также графически в виде многоугольника распределений.

9.1.9 Распределение непрерывных случайных величин

Закон распределения нельзя строить для непрерывной случайной величины. Поэтому наиболее общей формой закона распределения величины Х является функция распределения (интегральная функция). – вероятность того, что случайная точка Х в результате опыта попадает левее точки .

Для дискретной величины Х .

Свойства.

1.

2.

3. - неубывающая функция

4.

В дальнейшем величину Х считаем непрерывной, если - непрерывна.

Более наглядное представление, чем , о характере распределения непрерывной величины Х в окрестностях различных точек дается функцией плотности распределения (дифференциальной функцией) .

Свойства

1.

2.

3.

4.

9.1.10 Числовые характеристики случайной величины

Числовые характеристики выражают наиболее существенные особенности данного распределения.

Определение 18. Математическим ожиданием случайной величины Х называется

а) Х – дискретная величина

б) Х – непрерывная величина

Математическое ожидание можно рассматривать, как центр рассеивания величины Х. Если проводится 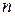опытов, то приближенно равна среднему арифметическому наблюдаемых значений Х.

Основными характеристиками случайной величины Х являются также рассеивание около , называемое дисперсией, и среднее квадратическое отклонение .

Определение 19. Дисперсией случайной величины Х называется число :

а) Х – дискретная

б) Х – непрерывная величина

Кроме указанных числовых характеристик используются и другие: мода, медиана, моменты и др.

Начальные и центральные теоретические моменты.

Определение 20. Начальным моментом порядка к случайной величины Х называют маматическое ожидание величины Х^к:

Аналогично для дисперсии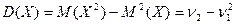

Определение 21. Центральным моментом порядка к случайной величины Х называют математическое ожидание величины :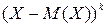

Легко выводятся связь между и

9.1.11 Распределение непрерывных случайных величин

1. Закон равномерного распределения вероятностей.

Определение 22. Распределение называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, дифференциальная функция .

Найдем дифференциальную функцию нормального распределения, считая, что , где 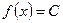. Поэтому при 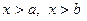. По свойству дифференциальной функци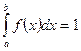и или или . Следовательно,

.

2. Нормальное распределение.

Определение 23. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается дифференциальной функцией

.

Здесь два параметра и 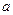. Их смысл: 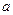- математическое ожидание, -средне квадратическое отклонение нормального распределения.

а)

.

б) = /дважды по частям/ = средне квадратическое отклонение.

Замечание 1). Если , то нормальное распределение называется нормированным. Дифференциальная функция его , а интегральная функция .

2). Известен интеграл Лапласа , тогда для нормального распределения.

3). Учитывая свойство , получим , т.е. .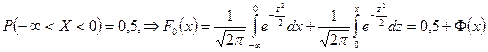

3. Вероятность попадания в заданный интервал нормальной случайной величины.

Известна формула , для нормального распределения имеем ,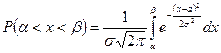

преобразуем эту формулу так, чтобы пользоваться готовыми таблицами

.Из этой формулы вытекает вероятность заданного отклонения .