Теоретический материал к разделу

Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении статистических данных – результатах наблюдений.

Основная задача математической статистики – указать способы сбора и группировки статистических сведений.

Другая задача математической статистики - разработка методов анализа статистических данных в зависимости от целей исследования.

10.1.1 Понятие о выборочном методе исследования.

Существует метод сплошного обследования исследуемой совокупности объектов, т.е. каждый объект обследуется относительно признака, который нужен. На практике этот метод применяется редко. Этот метод неприменим в силу обстоятельств: если обследующих объектов большое количество, например хлопка в партии, или обследование материала связано с его уничтожением, например, ткань исследуется на прочность, в таких случаях проводить сплошное обследование не имеет смысла. Наиболее распространенный и применяемый часто на практике – выборочный метод.

Выборочный метод состоит в определении сводных характеристик (показателей) какой-либо статистической совокупности путем наблюдения не всех, а лишь части составляющих ее членов, взятых на выборку. Например, для определения среднего срока службы большой партии электрических лампочек отбирается сравнительно небольшая часть их и испытывается. Средний срок службы испытанных лампочек принимается за приближенное значение среднего срока службы лампочек во всей партии. Выбор n единиц из совокупности N объем должен быть «репрезентативным», т.е. должен производиться так, чтобы свойства членов, попавших в «выборку», правильно отражали соответствующие свойства всей совокупности. По закону больших чисел достаточно обширная выборка будет репрезентативной, если ее производить случайно: каждый объект выборки отобрал случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку.

Основная задача математической теории выборочного метода.

Определение 1. Все множество объектов, подлежащих контролю и исследованию, называется генеральной совокупностью.

Определение 2. Множество, случайным оборазом отобранных объектов, называется выборочной совокупностью.

Определение 3. Число объектов выборочной совокупности (или генеральной совокупности) называют объемом выборки (или генеральной совокупностью).

Например, если из 10000 деталей отобрано для контроля 100, то говорят N=10000 – генеральная совокупность, n=100 - объем выборки.

Обычно генеральная совокупность содержит конечное множество объектов. Но оно достаточно велико, поэтому при теоретических выводах объем генеральной совокупности часто предполагается бесконечным. Это оправдывается тем, что увеличение объема генеральной совокупности уже не сказывается на результатах отработки данных выборки.

Определение 4. Вариационным рядом выборки называется способ её записи, при котором элементы упорядочиваются по величине, т.е. записываются в ви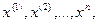де: где

Пусть в выборке объема n элемент встречается раз, то число называется частотой элемента , тогда

Определение 5. Статистическим рядом называется последовательность пар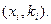

Обычно статистический ряд записывается в виде таблицы, первая строка содержит значения х, а вторая – соответствующие частоты. Статистическое распределение выборки можно задать также в виде последовательности интервалов и соответствующих им частот (суммы частот вариант, попавших в этот интервал).

10.1.2 Эмпирическая функция распределения

Для объектов генеральной совокупности определяется некоторая числовая характеристика – это случайная величина , принимающая на каждом объекте некоторое числовое значение. Сделав выборку, мы получаем ряд значений этой случайной величины . По этой последовательности значений нам следует приблизительно представить функцию распределения случайно величины , ее математическое ожидание и дисперсию.

В 1933г. советским математиком В.И. Гливенко была доказан основная теорема математической статистики, из которой следует правило для приближенного получения функции распределения случайной величины . Смысл ее в следующем: для любого действительного числа х обозначим частот чисел из выборки , удовлетворяющих неравенству . Этим на всей числовой прямой определена функция . Положим . Эта функция называется функцией распределения выборки случайной величины . Она и дает приближенную функцию распределения 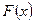случайно величины .

Определение 6. Функция называется функцией распределения выборки случайной величины .

Она дает приближенную функцию распределения 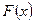случайно величины .

Свойства эмпирической функции распределения:

1. Значения

2. - неубывающая функция.

3. Если - наименьшая варианта, - наибольшая варианта, то =0 при

x< , =1 при x> .

10.1.3 Полигон и гистограмма

Кроме эмпирической функции распределения и ее графика бывает полезно изобразить аналог плотности вероятности. Это делают двумя способами. Для каждого подсчитывают частоту 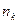. Откладывая на координату плоскости эти значения, проводят ломанную, которая называется полигон частот. Это график дает понятие о том, насколько часто встречается каждое значение. Вместо частоты и строится соответствующий полигон. Он отличен от предыдущего только изменением масштаба по оси ОУ.

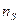Более наглядной представление о случайно величине дает гистограмма частот (относительных частот). Для ее построения весь промежуток разбивается на равные промежутки длины . Для каждого из них подсчитывается число наблюденных значений, в него попавших. Если на промежутке число значений , то строится прямоугольник с основанием и высотой . Получается чертеж, называющийся гистограммой частот. Площадь всего многоугольника равна числу всех наблюдаемых явлений, т.е. объему выборки.

Определение 7. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины , а высоты - (плотность частоты). Площадь гистограммы частот равна сумме выборки.

По гистограмме уже можно себе представить плотность вероятности случайной величины, а по эмпирическим функциям распределения – приближенную теоретическую функцию распределения.

10.1.4 Точечные оценки параметров.

Выведем приближенные формулы числовых характеристик случайной величины, математического ожидания и дисперсии.

Для математического ожидания случайной величины, для которой были зарегистрированы значения , принято брать значение

(1)

Число называется эмпирическим (выборочным) математическим ожиданием или средним по выборке.

Для дисперсии в качестве приближенного значения принято брать

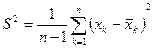(2)

Число 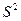называется эмпирической (выборочной) дисперсией.

10.1.5 Доверительные интервалы.

Точечные оценки параметров распределения являются первоначальными ориентировочными результатами обработки наблюдений. Их недостаток в том, что неизвестно, с какой степенью точности они дают оцениваемый параметр. Если для большого числа наблюдений обычно бывает достаточной для практических выводов (в силу несмещенность, состоятельности, эффективности), то для выборок с малым объемом вопрос о точности оценок очень существенен.

Поставленная задача в математической статистике решаются так. Пусть - неизвестный параметр распределения. По сделанной выборке находят числа 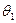и так, чтобы выполнялось равенство: .

Числа 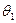и называются доверительными границами, а интервал доверительным интервалом для параметров . Число называется надежностью сделанной оценки.

За обычно принимается 0,95; 0,99; 0,999. Тогда практически достоверно, что . Поэтому число будет давать нам значение с точностью и практически достоверно.

Замечание. Числа 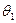и найдены по выборке , следовательно, сами – случайные величины. То есть интервал тоже случаен. Он может покрывать или не покрывать параметр . Именно в таком смысле понимают случайное событие , состоящее в том, что доверительный интервал покрывает число .