Тогда вероятность появления события ровно раз в испытаниях определяется формулой Бернули

Определения.

2. Если в результате опыта событие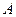

а) всегда произойдет, то 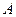- достоверное событие,

б) никогда не наступит, то 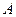- невозможные событие,

в) может произойти, то может и не произойти, то 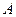- случайное (возможное) событие.

3. События называются равновозможным, если есть основания считать, что ни одно из этих событий не имеет больше шансов появиться в результате опыта, чем другие.

4. События 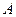и 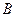- совместные (несовместные), если появление одного из них не исключает (исключает) появление другого.

5. Группа событий совместна, если совместны хотя бы два события из этой группы, иначе – несовместна.

6. Группа событий называется полной, если в результате опыта обязательно наступит одно из них.

9.1.2.Классическая и статистическая вероятность

Классический способ определения вероятности применяется для полной группы равновозможных несовместных событий. Вероятность – это мера объективной возможности данного события. Каждое событие этой группы назовем случаем или элементарным исходом. Каждое событие этой группы назовем случаем или элементарным исходом. По отношению к каждому событию случаи делятся на благоприятные и неблагоприятные.

Определение 7. Вероятностью 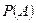события 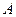называют величину

,

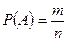где 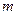- число случаев, благоприятных появлению события 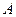, 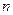- общее число равновозможных в данном опыте случаев.

Слабыми сторонами классического определения являются:

1. 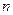- количество случаев конечно.

2. Результат опыта очень часто невозможно представить в виде совокупности элементарных событий (случаев).

3. Трудно указать основания, позволяющие считать случаи равновозможными.

Определение 8. Относительной частотой события 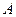называют величину

,

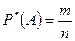где 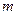- число испытаний, в которых появилось события 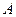, 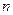- общее число испытаний.

Длительные наблюдения показали, что в различных опытах при достаточно больших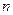

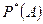изменяется мало, колеблясь около некоторого постоянного числа, которое назовем статистической вероятностью.

Вероятность обладает следующими свойствами:

1. Вероятность достоверного события равна 1.
2. Вероятность невозможного события равна 0.
3. Для любого события

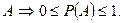
9.1.3 Алгебра событий

Определения.

9. Суммой или объединением нескольких событий называется событие, состоящее хотя бы одного из них.

10. Произведением нескольких событий, называется событие, состоящее в совместном появлении всех этих событий.

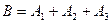- хотя бы одно попадание при трех выстрелах,

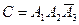- попадание при первым и вторым выстрелах и промах при третьем.

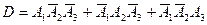- ровно одно попадание.

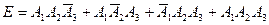- не менее двух попаданий.

11. Два события называется независимыми (зависимыми), если вероятность одного из них не зависит (зависит) от появления или не появления другого.

12. Несколько событий называются независимыми в совокупности, если каждое из них и любая линейная комбинация из остальных событий, есть события независимые.

13. Условной вероятностью 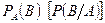называют вероятность события 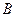, вычисленного в предположении, что событие 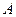произошло.

Теорема умножения вероятностей. Вероятность совместного появления (произведе-ния) нескольких событий равна произведению вероятности одного из них на условные вероятности остальных событий, вычисленных в предположении, что все предыдущие события имели место

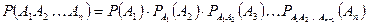
Следствие 1. Если 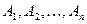- независимы в совокупности, то

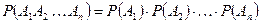
Действительно: так как .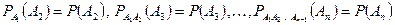

Теорема сложения вероятностей. Вероятность появления хотя бы одного из событий 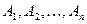равна

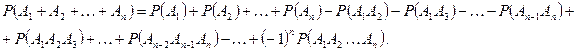
Следствие 2. Если события 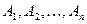попарно несовместные, то

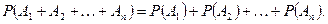
Действительно в этом случае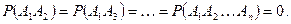

Следствие 3. Если попарно несовместные события 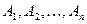образуют полную группу, то

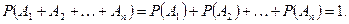
Определение 14. Противоположными называются два единственно возможных события.

Они обозначаются А и Ā.

Следствие 4. Для противоположных событий

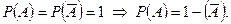
Следствие 5. Вероятность появления хотя бы одного из событий 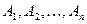, независимых в совокупности равна

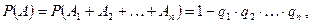(1)

где 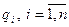- вероятности появления событий .

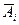В случае, если 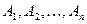имеют одинаковую вероятность 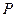, то формула (1) имеет вид 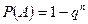, где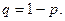

9.1.4 Формула полной вероятности

Задача 1. Пусть событие 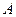может наступить или не наступить с одним из несовместных событий (гипотез) 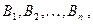образующих полную группу. Пусть известны 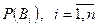и условные вероятности 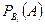. Тогда справедлива формула полной вероятности

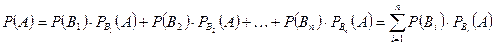(2)

9.1.5 Формула Бейеса

Предположим, что при условиях задачи 1 произведено испытание, в результате которого появилось событие 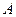. Как изменится вероятности гипотез в связи с появлением .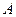

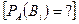Теорема гипотез (формула Бейеса). Вероятности гипотез после испытания равна

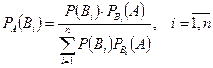. (3)

9.1.6 Повторение независимых испытаний. Формула Бернулли. Теоремы Лапласа. Формула Пуассона

Если производится несколько испытаний, в результате которых может появится событие в каждом испытании не зависит от исходов других испытаний, то эти испытания будут называться независимыми от. В этом пункте посылаем, что в одинаковых условиях производится независимых испытаний, в каждом из которых событие наступает с постоянной вероятностью.

Тогда вероятность появления события ровно раз в испытаниях определяется формулой Бернули

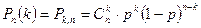(4)