 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Показательные и полиномиальные сравнения. 2 страница
|
|
4)  , 5)
, 5)  .
.
5.3. Решите полиномиальные сравнения, предварительно понизив их степени с помощью теоремы Ферма:
1) 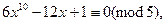 2)
2)  ,
,
3)  ,
,
4)  ,
,
5)  .
.
5.4. Докажите, что сравнение  не имеет решений.
не имеет решений.
5.5. Решите следующие сравнения:
1)  2)
2)  , 3)
, 3)  ,
,
4)  , 5)
, 5)  .
.
5.6. Решите следующие полиномиальные сравнения:
1)  2)
2)  ,
,
3)  ,
,
4)  ,
,
5) 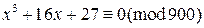 .
.
5.7. Решите следующие уравнения в натуральных числах
1)  , 2)
, 2)  , 3)
, 3)  .
.
5.8. Для каждого натурального  найдите число вычетов в полной системе вычетов по модулю
найдите число вычетов в полной системе вычетов по модулю  , удовлетворяющих сравнению
, удовлетворяющих сравнению  .
.
5.9. Докажите, что нахождение решений сравнения ax 2+ bx + c ≡ ≡0(mod m),  , сводится к нахождению решений сравнения вида
, сводится к нахождению решений сравнения вида  .
.
5.10. В приведенной системе вычетов по модулю 23 найдите все квадратичные вычеты.
5.11. Используя свойства символов Лежандра и Якоби, исследовать на разрешимость сравнения:
1)  , 2)
, 2)  , 3)
, 3)  ,
,
4)  , 5)
, 5)  .
.
5.12. Укажите способ решения показательного сравнения  , где
, где  .
.
5.13. Укажите способ решения степенного сравнения  , где
, где 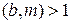 .
.
5.14. Пусть 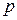 - простое число вида
- простое число вида 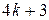 . Для любого целого
. Для любого целого 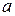 найдите решение сравнения
найдите решение сравнения  в явном виде.
в явном виде.
Группы.
Непустое множество  с заданной на нем бинарной операцией
с заданной на нем бинарной операцией  образует группу
образует группу  , если выполнены условия:
, если выполнены условия:
1) операция  ассоциативна, то есть
ассоциативна, то есть  для любых
для любых  ;
;
2) существует нейтральный элемент  , то есть
, то есть 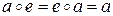 для любого
для любого 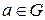 ;
;
3) для любого элемента 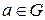 существует обратный элемент
существует обратный элемент  , то есть
, то есть  .
.
Если операция  коммутативна, то есть
коммутативна, то есть 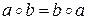 для любых
для любых  , то группа
, то группа  называется коммутативной или абелевой. Если множество
называется коммутативной или абелевой. Если множество  конечное, то группа
конечное, то группа  называется конечной, а число элементов множества
называется конечной, а число элементов множества  называется порядком группы
называется порядком группы  и обозначается
и обозначается  . Для любого целого числа
. Для любого целого числа 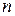 степень
степень  элемента
элемента 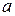 определяется следующим образом:
определяется следующим образом:  ,
,  для натуральных
для натуральных 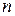 ,
,  . Натуральное число
. Натуральное число 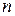 называется порядком элемента
называется порядком элемента 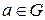 и обозначается
и обозначается  , если
, если  и
и  для любого натурального
для любого натурального  , меньшего
, меньшего 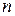 . Если группа
. Если группа  конечна, то для вычисления порядка степеней элементов справедлива формула:
конечна, то для вычисления порядка степеней элементов справедлива формула:  ,
,  .
.
Если в группе  существует элемент
существует элемент 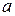 , такой, что для любого элемента
, такой, что для любого элемента  существует целое число
существует целое число 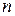 , такое, что
, такое, что  , то группа
, то группа  называется циклической, а элемент
называется циклической, а элемент 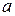 называется образующим элементом группы
называется образующим элементом группы  и обозначается
и обозначается  .
.
Пусть  - непустое подмножество множества G.
- непустое подмножество множества G.
Если множество  образует группу относительно операции
образует группу относительно операции  , то группу
, то группу  называют подгруппой группы
называют подгруппой группы  и пишут
и пишут  или
или 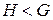 в случае
в случае  ; если же
; если же  и
и  для любых
для любых 
 , то говорят, что
, то говорят, что  - нормальная подгруппа (нормальный делитель) группы
- нормальная подгруппа (нормальный делитель) группы  и обозначают
и обозначают  .
.
Пусть  . Тогда для каждого элемента
. Тогда для каждого элемента 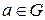 множества
множества  ,
,  называются соответственно левым смежным классом и правым смежным классом. В случае
называются соответственно левым смежным классом и правым смежным классом. В случае  левый смежный класс
левый смежный класс  совпадает с правым смежным классом
совпадает с правым смежным классом  и называется смежным классом по нормальной подгруппе.
и называется смежным классом по нормальной подгруппе.
Если  , то для любых элементов
, то для любых элементов  смежные классы
смежные классы  ,
,  либо не пересекаются, либо совпадают и мощность каждого смежного класса равна мощности множества
либо не пересекаются, либо совпадают и мощность каждого смежного класса равна мощности множества  .Если
.Если  – множество всех различных смежных классов, то
– множество всех различных смежных классов, то  образует группу относительно операции
образует группу относительно операции  умножения смежных классов и
умножения смежных классов и  .
.
Группа 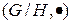 называется фактор-группой группы
называется фактор-группой группы  по подгруппе
по подгруппе  ; нейтральным элементом фактор-группы
; нейтральным элементом фактор-группы 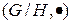 является множество
является множество  , а обратным элементом к
, а обратным элементом к  является смежный класс
является смежный класс  ; число элементов в фактор-группе
; число элементов в фактор-группе 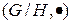 , в случае её конечности, называется индексом подгруппы
, в случае её конечности, называется индексом подгруппы  в группе
в группе  и обозначается
и обозначается  . В случае конечности группы
. В случае конечности группы  имеет место равенство
имеет место равенство  (теорема Лагранжа).
(теорема Лагранжа).
Пусть  и
и  - группы; отображение
- группы; отображение  называется гомоморфизмом групп, если
называется гомоморфизмом групп, если 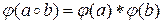 для любых
для любых  ; ядром гомоморфизма
; ядром гомоморфизма  называется множество
называется множество  , где
, где  - нейтральный элемент группы
- нейтральный элемент группы  ; образом гомоморфизма
; образом гомоморфизма  называется множество
называется множество  ; ядро гомоморфизма
; ядро гомоморфизма 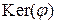 образует нормальную подгруппу группы
образует нормальную подгруппу группы  , образ гомоморфизма
, образ гомоморфизма  образует подгруппу группы
образует подгруппу группы  ; биективный гомоморфизм называется изоморфизмом; группы
; биективный гомоморфизм называется изоморфизмом; группы  и
и  называются изоморфными, если существует изоморфизм
называются изоморфными, если существует изоморфизм  , и обозначают
, и обозначают  ; для любого гомоморфизма
; для любого гомоморфизма  группы
группы  и
и  являются изоморфными (теорема об изоморфизме); любая конечная циклическая группа порядка
являются изоморфными (теорема об изоморфизме); любая конечная циклическая группа порядка 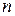 изоморфна группе вычетов
изоморфна группе вычетов  по модулю
по модулю 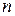 , любая бесконечная циклическая группа изоморфна аддитивной группе целых чисел
, любая бесконечная циклическая группа изоморфна аддитивной группе целых чисел  .
.
Пример 1. Определите, образует ли группу множество 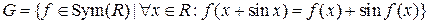 с операцией суперпозиции.
с операцией суперпозиции.
Решение. Проверим, что операция суперпозиции является бинарной операцией на множестве  , т.е.
, т.е.  для любых
для любых 
 . Так как
. Так как  , то
, то  . Кроме того, для любого
. Кроме того, для любого 

 .
.
Очевидно, операция суперпозиции является ассоциативной. Нейтральным элементом является тождественное отображение:  ,
,  . Покажем, что обратным элементом к
. Покажем, что обратным элементом к  является обратное отображение
является обратное отображение  . Так как
. Так как  , то
, то  . Возьмём произвольное
. Возьмём произвольное  и обозначим
и обозначим  , тогда
, тогда  ,
,  . Так как
. Так как  , то
, то  . Следовательно,
. Следовательно,  . Отсюда получаем
. Отсюда получаем  . Множество
. Множество  с операцией суперпозиции образует группу.
с операцией суперпозиции образует группу.
Пример 2. Найдите все подгруппы группы  .
.
Решение. Докажем, что любая подгруппа группы  имеет вид
имеет вид  , где
, где  ,
,  - некоторый натуральный делитель числа
- некоторый натуральный делитель числа 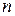 . Пусть
. Пусть  - произвольная подгруппа группы
- произвольная подгруппа группы  ,
,  - наименьший натуральный вычет множества
- наименьший натуральный вычет множества  . Допустим, существует такой элемент
. Допустим, существует такой элемент  , что
, что  не делится на
не делится на  , то есть
, то есть  , где
, где  ,
,  . Но тогда
. Но тогда  , что противоречит минимальности
, что противоречит минимальности  . Следовательно, для любого
. Следовательно, для любого  найдётся натуральное
найдётся натуральное  , такое, что
, такое, что  . Допустим, что
. Допустим, что 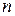 не делится на
не делится на  , тогда
, тогда  , где
, где 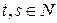 ,
,  . Отсюда
. Отсюда  , что противоречит минимальности
, что противоречит минимальности  . Следовательно,
. Следовательно,  есть подмножество множества
есть подмножество множества  . Очевидно,
. Очевидно,  .
.
Пример 3. Определите, являются ли группы  и
и  изоморфными.
изоморфными.
Решение. Обозначим  ,
,  . Отображение
. Отображение  , действующее по правилу
, действующее по правилу  ,
,  , является гомоморфизмом, так как
, является гомоморфизмом, так как

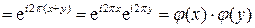 .
.
Так как гомоморфизм  биективный, то группы
биективный, то группы  ,
,  являются изоморфными.
являются изоморфными.
Пример 4. Пусть  - циклическая группа 8-го порядка,
- циклическая группа 8-го порядка,  - её подгруппа порядка 4. Найдите индекс подгруппы
- её подгруппа порядка 4. Найдите индекс подгруппы  в группе
в группе  и вычислите фактор-группу
и вычислите фактор-группу  .
.
Решение. Пусть 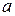 - образующий элемент группы
- образующий элемент группы  , тогда
, тогда  . Так как
. Так как  , то
, то  , где
, где  - некоторый делитель числа 8. Поскольку
- некоторый делитель числа 8. Поскольку  , то
, то  . Следовательно,
. Следовательно,  . Индекс
. Индекс  равен 2. Фактор-группа
равен 2. Фактор-группа  состоит из двух смежных классов
состоит из двух смежных классов  и
и  .
.
6.1. Определите, какие из указанных множеств относительно заданных операций, образуют группу:
1)  , где
, где  - одно из множеств
- одно из множеств 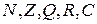 ;
;
2)  , где
, где  - одно из множеств
- одно из множеств 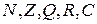 ;
;
3)  , где
, где  - одно из множеств
- одно из множеств 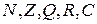 ;
;
4)  , где
, где  - одно из множеств
- одно из множеств  ;
;
5)  , где
, где  - одно из множеств
- одно из множеств  (
( - множество всех положительных чисел из множества
- множество всех положительных чисел из множества  );
);
Дата публикования: 2015-11-01; Прочитано: 676 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
