 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Показательные и полиномиальные сравнения. 1 страница
|
|
Рассмотрим показательное сравнение  (5.1), где
(5.1), где 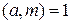 . Условие
. Условие  является необходимым для разрешимости сравнения (5.1). Пусть
является необходимым для разрешимости сравнения (5.1). Пусть  - каноническое разложение модуля
- каноническое разложение модуля 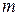 , где
, где  может быть нулем. Сравнение (5.1) равносильно системе сравнений:
может быть нулем. Сравнение (5.1) равносильно системе сравнений:  ,
,  ,
,  (5.2). Пусть
(5.2). Пусть 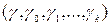 ,
,  - системы индексов соответственно чисел
- системы индексов соответственно чисел 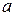 и
и 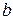 по модулю
по модулю 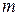 , то есть
, то есть 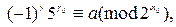
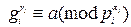 ,
,
(–1) d 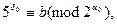
 , где
, где  - первообразный корень по модулю
- первообразный корень по модулю  (
( ). Тогда система (5.2) эквивалентна системе сравнений первого порядка:
). Тогда система (5.2) эквивалентна системе сравнений первого порядка: 

 ,
,  , (5.3) где
, (5.3) где 

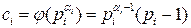 ,
,  . Решение системы (5.3), если оно существует, может быть найдено с помощью китайской теоремы об остатках.
. Решение системы (5.3), если оно существует, может быть найдено с помощью китайской теоремы об остатках.
Пример 1. Решите показательное сравнение  .
.
Решение. Найдем системы индексов чисел  и
и  по модулю
по модулю 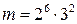 . Используя таблицу индексов
. Используя таблицу индексов

| ||||||||||||||||
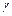
| ||||||||||||||||
|

| ||||||||||||||||
| ||||||||||||||||
|
по модулю 64, находим, что 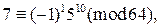
 . Так как
. Так как 
 ,
, 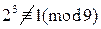 , то число 2 является первообразным корнем по модулю 9. Учитывая, что
, то число 2 является первообразным корнем по модулю 9. Учитывая, что  ,
,  , делаем вывод о том, что
, делаем вывод о том, что  ,
,  - системы индексов соответственно чисел
- системы индексов соответственно чисел 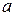 и
и 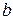 по модулю
по модулю 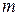 . Следовательно, сравнение
. Следовательно, сравнение  равносильно системе сравнений
равносильно системе сравнений
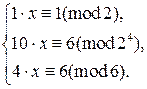
Разрешая эту систему, находим, что  .
.
Другой подход к решению показательного сравнения (5.1) заключается в использовании свойств показателей и применении китайской теоремы об остатках. Проиллюстрируем этот приём на следующем примере.
Пример 2. Решите показательное сравнение  .
.
Решение. Так как  , то сравнение
, то сравнение  равносильно системе сравнений:
равносильно системе сравнений:

Показатель  , которому принадлежит число 5 по модулю
, которому принадлежит число 5 по модулю 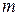 делит
делит 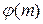 . Отсюда находим, что
. Отсюда находим, что  ,
,  ,
,  . Так как
. Так как  ,
,  ,
, 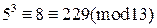 имеем:
имеем:

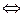

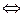

Применяя к последней системе китайскую теорему об остатках, получаем 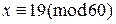 .
.
Укажем способ решения степенного сравнения  (5.4), где
(5.4), где  . Пусть
. Пусть  - каноническое разложение модуля
- каноническое разложение модуля 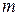 , где
, где  , тогда сравнение (5.4) эквивалентно системе сравнений:
, тогда сравнение (5.4) эквивалентно системе сравнений:  ,
,  ,
,  . Пусть
. Пусть 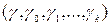 ,
,  - системы индексов соответственно чисел
- системы индексов соответственно чисел 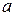 и
и 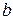 по модулю
по модулю 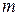 , то есть
, то есть 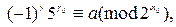
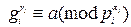 ,
, 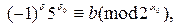
 , где
, где  - первообразный корень по модулю
- первообразный корень по модулю  . Тогда система индексов
. Тогда система индексов  числа
числа 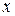 по модулю
по модулю 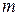 может быть найдена из следующих сравнений:
может быть найдена из следующих сравнений: 


 . Решение сравнения (5.4) можно найти из системы:
. Решение сравнения (5.4) можно найти из системы: 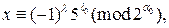
 ,
,  .
.
Пример 3. Решите степенное сравнение  .
.
Решение. Найдем системы индексов чисел  ,
,  по модулю
по модулю  . Имеем
. Имеем  ,
, 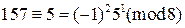 ;
; 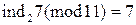 ,
,  ;
;  ,
,  . Следовательно,
. Следовательно,  и (2,1,8,12) – системы индексов чисел 7 и 157 по модулю
и (2,1,8,12) – системы индексов чисел 7 и 157 по модулю  . Для нахождения системы индексов неизвестного числа
. Для нахождения системы индексов неизвестного числа 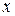 получаем систему сравнений:
получаем систему сравнений:

Решая систему, находим, что  - система индексов числа
- система индексов числа 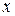 . Получаем систему сравнений для нахождения
. Получаем систему сравнений для нахождения 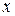 :
:

Используя китайскую теорему об остатках, получаем, что  .
.
Перейдем к рассмотрению полиномиальных сравнений  (5.5), где
(5.5), где  ,
,  для любого
для любого  . Сравнение (5.5) равносильно системе сравнений
. Сравнение (5.5) равносильно системе сравнений  ,
,  , где
, где  - каноническое разложение модуля
- каноническое разложение модуля 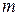 . Таким образом, для решения сравнения (5.5) следует решить каждое из сравнений
. Таким образом, для решения сравнения (5.5) следует решить каждое из сравнений  , а затем применить китайскую теорему об остатках.
, а затем применить китайскую теорему об остатках.
Приведем способ нахождения решения полиномиального сравнения  по примарному модулю.
по примарному модулю.
1) Применяя теорему Ферму, сравнение  сводим к полиномиальному сравнению
сводим к полиномиальному сравнению  , где
, где  - многочлен с целыми коэффициентами степени не выше, чем
- многочлен с целыми коэффициентами степени не выше, чем  . Находим решения сравнения
. Находим решения сравнения  :
: 
 .
.
2) Для каждого фиксированного  полагаем
полагаем  , где
, где  . Левую часть сравнения
. Левую часть сравнения  раскладываем по формуле Тейлора (принимая во внимание, что число
раскладываем по формуле Тейлора (принимая во внимание, что число  является целым, и отбрасывая члены, кратные
является целым, и отбрасывая члены, кратные  ):
):  . Сокращая обе части сравнения и модуль на
. Сокращая обе части сравнения и модуль на 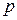 , получаем:
, получаем:  . Находим решения этого сравнения:
. Находим решения этого сравнения:  ,…,
,…,  . Таким образом, x ≡ xi + ti,jp = xi, j(mod p 2),
. Таким образом, x ≡ xi + ti,jp = xi, j(mod p 2),  ,
,  .
.
3) Для каждых фиксированных  ,
,  полагаем
полагаем 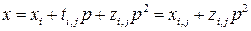 , где
, где  . Аналогично левую часть сравнения
. Аналогично левую часть сравнения  раскладываем по формуле Тейлора и отбрасываем члены, кратные
раскладываем по формуле Тейлора и отбрасываем члены, кратные  :
:  . Сокращая сравнение на
. Сокращая сравнение на  , получим:
, получим:  . Решая сравнение, находим, что
. Решая сравнение, находим, что  ,
,  . Подставляя в
. Подставляя в 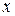 , получим:
, получим:  .
.
4) Проделывая последовательно для модулей  описанную процедуру, найдем решения
описанную процедуру, найдем решения  сравнения
сравнения  .
.
Отметим, что в случае  решение
решение  сравнения
сравнения  даст одно решение
даст одно решение  сравнения
сравнения  .
.
Пример 4. Решите полиномиальное сравнение 16x8–8x7+9x4–1≡ ≡0(mod196).
Решение. Исходное сравнение эквивалентно системе сравнений:

Из первого сравнения системы получаем:  . Обозначим
. Обозначим  . Найдем решение сравнения
. Найдем решение сравнения  . Имеем:
. Имеем: 
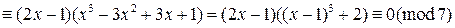 . Отсюда получаем, что
. Отсюда получаем, что  . Пусть
. Пусть  ,
,  .
.
Далее  . Следовательно,
. Следовательно,  . Таким образом,
. Таким образом,  - решение второго сравнения системы.
- решение второго сравнения системы.
Применяя китайскую теорему об остатках к системам

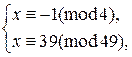
заключаем, что 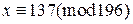 ,
,  .
.
Рассмотрим двучленное сравнение второй степени  (5.6), где
(5.6), где 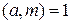 . Если сравнение (5.6) имеет решение, то число
. Если сравнение (5.6) имеет решение, то число 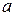 называется квадратичным вычетом по модулю
называется квадратичным вычетом по модулю 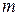 , в противном случае
, в противном случае 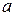 называется квадратичным невычетом по модулю
называется квадратичным невычетом по модулю 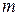 .
.
Пусть  , где
, где 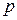 - нечетное простое число. Приведенная система вычетов по модулю
- нечетное простое число. Приведенная система вычетов по модулю 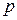 состоит из
состоит из  квадратичных вычетов и
квадратичных вычетов и  квадратичных невычетов. Символ Лежандра
квадратичных невычетов. Символ Лежандра  определяется равенством
определяется равенством  , если
, если 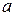 является квадратичным вычетомпо модулю
является квадратичным вычетомпо модулю 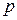 , и равенством
, и равенством  , если
, если 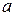 является квадратичным невычетомпо модулю
является квадратичным невычетомпо модулю 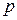 . Для любых
. Для любых  ,
,  и любого нечётного простого числа
и любого нечётного простого числа  ,
,  , имеют место следующие свойства:
, имеют место следующие свойства:
1)  ;
;
2) 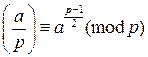 (критерий Эйлера);
(критерий Эйлера);
3)  ;
;
4)  ;
;
5)  (квадратичный закон взаимности).
(квадратичный закон взаимности).
Пусть теперь  - нечётное натуральное число, большее 1, и
- нечётное натуральное число, большее 1, и  - разложение числа
- разложение числа  на простые множители. Для всякого целого числа
на простые множители. Для всякого целого числа 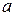 , взаимно простого с
, взаимно простого с  , символ Якоби
, символ Якоби  определяется через символы Лежандра по формуле:
определяется через символы Лежандра по формуле:  . Для любых целых
. Для любых целых 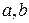 , взаимно простых с
, взаимно простых с  , и любого нечётного натурального
, и любого нечётного натурального  , большего 1 и взаимно простого с
, большего 1 и взаимно простого с  , имеют место следующие свойства символа Якоби:
, имеют место следующие свойства символа Якоби:
6)  ;
;
7)  ;
;
8)  ;
;
9)  ;
;
10)  ;
;
11)  .
.
Отметим, что равенство символа Якоби  единице является необходимым условием для того, чтобы число
единице является необходимым условием для того, чтобы число 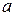 было квадратичным вычетом по модулю
было квадратичным вычетом по модулю  , но не достаточным.
, но не достаточным.
Пример 5. Исследовать на разрешимость сравнение  .
.
Решение. Вычислим символ Лежандра  , рассматривая его как символ Якоби и используя свойства символа Якоби:
, рассматривая его как символ Якоби и используя свойства символа Якоби:

 .
.
Откуда следует, что сравнение разрешимо.
5.1. Используя свойства показателей, решите следующие показательные сравнения по простому модулю:
1)  2)
2)  3)
3)  ,
,
4)  , 5)
, 5) 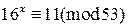 .
.
5.2. Используя свойства показателей и китайскую теорему об остатках, решите следующие показательные сравнения по составному модулю:
1)  2)
2)  3)
3)  ,
,
Дата публикования: 2015-11-01; Прочитано: 3757 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
