Функция двух случайных аргументов

Если каждой паре возможных значений случайных величин и по определенному правилу соответствует одно возможное значение случайной величины , то называют функцией двух случайных аргументов , и записывают .

Для случайной величины функция распределения вычисляется по формуле

, (72)

где 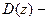область на плоскости , для которой .

Плотность распределения случайной величины находится дифференцированием функции распределения , т.е. .

Для практики большое значение имеет задача определения закона распределения суммы двух случайных величин, т.е. случайной величины .

Если и дискретные независимые величины, то случайная величина также является дискретной и определение ее закона распределения описано в разделе 2.1.1 данного пособия.

В частности, если представляет сумму двух независимых случайных величин, обе распределенных по закону Пуассона с параметрами и соответственно, то также распределена по закону Пуассона с параметром .

Если и непрерывные независимые величины и заданы своими плотностями распределения и 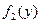соответственно, то плотность распределения суммы может быть найдена с помощью равенства

, (73)

либо с помощью равносильного равенства

. (74)

Формулы (72), (73) называют формулами композиции (свертки) двух распределений.

Если случайные величины , то плотность распределения находится по формуле

. (75)

Композиция нормальных законов распределения также имеет нормальное распределение. Так, если и независимые нормально распределенные величины, т.е. ~ , ~ , то случайная величина также нормально распределена: ~ .

В случае, если случайные величины и зависимы (коэффициент корреляции ), то случайная величина по- прежнему нормально распределена с параметрами: .

Характеристической функцией случайной величины называется функция

,

где произвольный, вещественный параметр, мнимая единица, символ математического ожидания.

Для дискретной случайной величины характеристическая функция определяется по формуле

, , (76)

а для непрерывной сумма заменяется интегралом

, (77)

где плотность распределения случайной величины .

Плотность распределения можно выразить через характеристическую функцию

.

Если случайные величины являются независимыми и , то характеристическая функция равна произведению характеристических функций 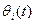слагаемых

. (78)

Пример 64. Система (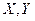) задана совместной плотностью распределения: внутри квадрата и вне квадрата. Найти функцию распределения их отношения .

Решение. Вначале рассмотрим общий случай для произвольной плотности .

Рис. 6

А   0 В   Рис. 7

Зададим некоторое значение и построим на плоскости область 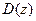, в которой (или ). При фиксированном значении уравнение описывает прямую, а область 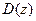представляет заштрихованную часть плоскости (рис. 6).

Тогда по формуле (72) запишем

.

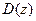В нашем случае вне квадрата , поэтому область представляется той частью этого квадрата, которая находится ниже прямой (рис. 7). Величина площади зависит от значения .

Если , то и . При площадь под прямой в квадрате равна нулю и . Итак, при имеем .

Пусть . Тогда область 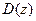представляет площадь треугольника 0АВ (рис. 7, заштрихованная область). Для определения возьмем двойной интеграл по этой площади

.

А В 0 D C Рис. 8

A F B   E K z   0 D C   z   Рис. 9

Заметим, что при значении имеем , а при функция .

Пусть . В этом случае область 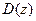будет представлена площадью треугольника 0AD и площадью прямоугольника ABCD (рис. 8).

Отсюда

.

Таким образом, искомая функция распределения имеет вид:

Пример 65. Независимые случайные величины и имеют равномерные распределения:

Найти функцию распределения и плотность распределения случайной величины .

Решение. По условию задачи случайные точки (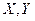) расположены в квадрате 0ABCD, задаваемом неравенствами (рис. 9). Зафиксируем значение . По определению функции распределения . Неравенству удовлетворяют те точки плоскости , которые лежат ниже прямой 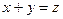и находятся в квадрате 0ABCD (рис. 9, заштрихованная область).

Поскольку и независимы, то и по формуле (72) имеем

,

где площадь той части квадрата 0ABCD, которая лежит ниже прямой, задаваемой уравнением 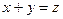. Величина зависит от значения .

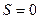Если , то и .

Пусть , тогда 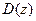представляет собой площадь треугольника oED и (рис. 9). Отсюда

.

Если , то 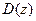представляет собой площадь фигуры 0AFKC, которую проще найти, вычитая из площади квадрата 0ABC (она равна ) площадь треугольника FBK.

Из рисунка видно, что площадь треугольника FBK находится

.

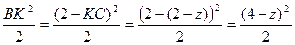Тогда

.

Наконец, если 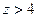, то 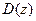совпадает с площадью квадрата 0ABCD и .

Итак, искомая функция распределения имеет вид:

Дифференцируя , определяем плотность распределения :

-

Пример 66. Случайные величины и распределены по показательному закону с плотностями распределения:

Найти плотность распределения случайной величины .

Решение. Поскольку обе случайные величины могут принимать только положительные значения, то для определения плотности можно воспользоваться формулой (75)

.

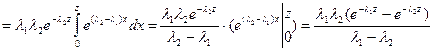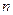Пример 67. Найти характеристическую функцию случайной величины , распределенной по биномиальному закону с параметрами и :

.

Решение. Представим как сумму 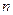независимых случайных величин

,

где случайная величина с рядом распределения

Характеристическая функция случайной величины вычисляется по формуле (76)

.

Так как характеристическая функция суммы независимых случайных величин равна произведению их характеристических функций, то искомая функция имеет вид

.

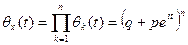Пример 68. Смешаны две группы однотипных деталей, содержащих и 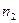деталей каждая. Число бракованных деталей в каждой группе (соответственно и ) имеют биномиальное распределение:

.

Найти ряд распределения случайной величины .

Решение. Решим задачу с помощью характеристических функций. Для случайных величин и имеем (см. пример 67):

.

Поскольку случайные величины и независимы, то характеристическая функция их суммы равна произведению характеристических функций и

.

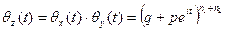т.е. случайная величина также имеет биномиальное распределение

.