Условие перпендикулярности плоскостей

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .

Таким образом, .

Примеры.

1. Составить уравнение плоскости, проходящей через точку

M (-2; 1; 4) параллельно плоскости 3x +2 y -7 z +8=0.

Уравнение плоскости будем искать в виде Ax+By+Cz+D =0. Из условия параллельности плоскостей следует, что: 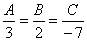. Поэтому можно положить A =3, B =2, C =-7. Поэтому уравнение плоскости принимает вид3x+2y-7z+D=0.

Кроме того, так как M  α, то-6+2-28+D=0, D=32.

Итак, искомое уравнение 3 x +2 y -7 z +32=0.

1. Составить уравнение плоскости, проходящей через точки M₁ (1; 1; 1), M₂ (0; 1; –1) перпендикулярно плоскости x+y+z =0.

Так как M₁  α, то используя уравнение плоскости, проходящей через заданную точку, будем иметь A (x -1)+ B (y -1)+ C (z -1)=0.

Далее, так как M₂  α, то подставив координаты точки в выписанное уравнение, получим равенство -A -2 C =0 или A +2 C =0.

Учтем, что заданная плоскость перпендикулярна искомой. Поэтому A+B+C =0.

Выразим коэффициенты A и B через C: A =-2 C, B=C и подставим их в исходное уравнение: -2 C (x -1)+ C (y -1)+ C (z -1)=0.

Окончательно получаем -2 x + y+z =0.

1. Составить уравнение плоскости, проходящей через точку M (-2; 3; 6) перпендикулярно плоскостям 2 x +3 y -2 z -4=0 и 3 x +5 y + z =0.

Так как M  α, то A (x +2)+ B (x -3)+ C (z -6)=0.

По условию задачи , поэтому

Итак уравнение плоскости принимает вид 13(x +2)-8(y -3)+ z -6=0 или 13 x -8 y + z+ 44=0.