 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Четность подстановки
|
|
Определение 6. Пусть  — разложение подстановки
— разложение подстановки  в произведение транспозиций. Тогда число
в произведение транспозиций. Тогда число  называется знаком 7)(четностью) подстановки
называется знаком 7)(четностью) подстановки  . Подстановка называется четной 8), если
. Подстановка называется четной 8), если  и нечетной 9) в противном случае.
и нечетной 9) в противном случае.
Предложение 3. Четность подстановки не зависит от способа разложения подстановки в произведение транспозиций.
Предложение 4. Для двух подстановок  и
и 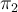 четность их произведения равна произведению четностей:
четность их произведения равна произведению четностей:

Доказательство.
Пусть  ,
,  , значит,
, значит,  и
и  . Тогда
. Тогда  — разложение подстановки в произведение транспозиций. Поэтому
— разложение подстановки в произведение транспозиций. Поэтому
 .
.
Предложение 5. Пусть  — цикл длины
— цикл длины  . Тогда его четность равна
. Тогда его четность равна  .
.
Доказательство.
Утверждение следует из того, что цикл длины  представим в виде произведения
представим в виде произведения  -й транспозиции
-й транспозиции

Утверждение следует из того, что цикл длины  представим в виде произведения
представим в виде произведения  -й транспозиции
-й транспозиции
 .
.
Определение 7. Пусть  — разложение подстановки в произведение независимых циклов длин
— разложение подстановки в произведение независимых циклов длин  . Число
. Число  называется декрементом 10) подстановки
называется декрементом 10) подстановки  .
.
Предложение 6. Пусть  — разложение подстановки в произведение независимых циклов длин
— разложение подстановки в произведение независимых циклов длин  . Тогда четность подстановки
. Тогда четность подстановки  вычисляется по формуле
вычисляется по формуле
 .
.
По предложению 5  для
для  . По предложению 4
. По предложению 4
 .
.
Пример 6. Любая транспозиция — это нечетная подстановка. Подстановка из примера 4 нечетная, так как декремент  — нечетное число.
— нечетное число.
Пример 7. Любая подстановка, в разложении которой на независимые циклы все циклы имеют нечетные длины  , четна, так как ее декремент — это сумма
, четна, так как ее декремент — это сумма  четных чисел
четных чисел 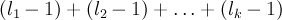 .
.
Дата публикования: 2015-11-01; Прочитано: 1495 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
