Вычисление частотных характеристик звена или системы

Пусть задана передаточная функция звена, например:

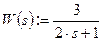
Найдём комплексный коэффициент передачи, заменив переменную s на jw. Для этого введём мнимую единицу .

Для этого заменим s (оператор Лапласа) на (jω): 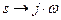с учетом того, что 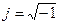и путем несложных преобразований - подстановку комплексной переменной и перемножение числителя и знаменателя на комплексно сопряженное число получим:

,

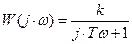Избавляясь от мнимой единицы j в знаменателе (иррациональности), получаем комплексный коэффициент передачи в виде:

.

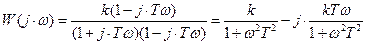Вещественная часть ККП:	Мнимая часть ККП:
.	.

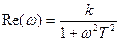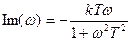Запишем комплексный коэффициент передачи формальной заменой s на jω в передаточной функции разомкнутой системы и выведем полученное выражение на экран с помощью «символьной стрелки», вызываемой также из палитры Символьные операторы:

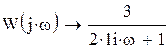
Для нахождения вещественной 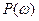и мнимой 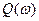частотных характеристик звена воспользуемся стандартными функциями Mathcad: Re() и Im() соответственно:

,

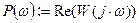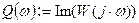
Для нахождения вещественной и мнимой частей выражения в Mathcad имеются специализированные встроенные функции:

Выбрать из командной строки опцию «вставка функции» f(x) и из предложенного списка слева – категория функции – комплексные числа (Complex Number), из предложенного списка справа – имя функции Re() или Im() – далее клик по кнопке «ОК» или «добавить».

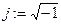
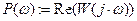
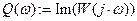
Однако возможности Mathcad не позволяют сразу получить комплексный коэффициент передачи в виде суммы вещественной и мнимой частей.

При этом следует учесть, что комплексный коэффициент передачи может быть представлен в виде

,

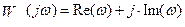где 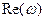- вещественная часть комплексного коэффициента передачи,

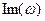- мнимая часть комплексного коэффициента передачи.

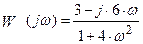
Тогда мнимая и вещественная части будут равны:

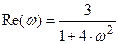
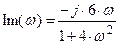
Для построения годографа АФЧХ звена зададим диапазон и шаг изменения аргумента w (частоты), воспользовавшись знаком «многоточие», вызываемым с помощью символа «;»:

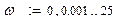
Далее из палитры Инструменты графиков вызовем поле декартовых координат (Ctrl+2), где в позиции на оси абсцисс запишем P (ω), а на оси ординат – Q (ω):

Для построения вещественной 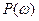и мнимой 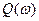частотных характеристик звена зададим диапазон и шаг изменения аргумента w (частоты), воспользовавшись знаком «многоточие», вызываемым с помощью символа «;»:

w: =0, 0.1.. 1000

Далее из палитры Инструменты графиков вызовем поле декартовых координат (Ctrl+2), где в позиции на оси абсцисс запишем w, а на оси ординат – P (ω) или Q (ω):

Теперь определим амплитудную-частотную (АЧХ) и фазовую частотную (ФЧХ) характеристики. По определению, АЧХ вычисляется как модуль комплексного коэффициента передачи, а ФЧХ - как его аргумент:

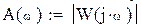
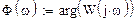
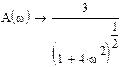
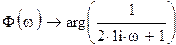
Действительная логарифмическая АЧХ в соответствии с определением вычисляется по формуле :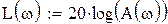

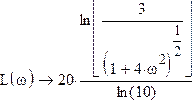Для построения логарифмических частотных характеристик из палитры Инструменты графиков вызовем поле координат (Ctrl+2), где в позиции на оси ординат запишем логарифмическую АЧХ L (w) или фазовую частотную характеристику F (w), а на оси абсцисс задаем логарифмический масштаб - lgw.

Далее произвести построение асимптотических логарифмических частотных характеристик системы автоматического регулирования по вариантам заданий 4-ой лабораторной работы в соответствии с методикой изложенной выше в п.4.2.4.