Инерционное (апериодическое) звено первого порядка

Передаточная функция инерционного звена равна

.

Комплексный коэффициент передачи звена будет:

Для нахождения вещественной и мнимой частотных характеристик инерционного звена представим это выражение в следующем виде: отсюда получим вещественную и мнимую частотные характеристики инерционного звена , . Из полученных зависимостей следует, что функция - четная, а функция - нечетная.

Для нахождения годографа АФЧХ инерционного звена, зависимости Q ₄(w) от P ₄(w), найдем уравнение в функции от переменных и .

Получим . Подставляя это выражение в формулу для Q ₄(w), находим: . Преобразуя эту зависимость, имеем: . Таким образом, годограф амплитудно-фазовой частотной характеристики (АФЧХ) инерционного звена представляет собой окружность

Учитывая известную связь между частотными характеристиками найдем амплитудно-частотную и фазовую частотные характеристики:

.

Действительная логарифмическая амплитудная частотная характеристика равна

Характеристика имеет низкочастотную и высокочастотную асимптоты, которые сопрягаются на частоте сопряжения .

Низкочастотная асимптота ЛАЧХ инерционного звена представляет собой предел, при этом и второе слагаемое ЛАЧХ равно нулю.

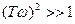Высокочастотная асимптота ЛАЧХ находится как из условия . Тогда и

.

Асимптотической ЛАЧХ является характеристика, составленная из асимптот - двух прямых линий: и

Графики и показаны на рис. 5.7.

Эти характеристики имеют следующие особенности:

низкочастотная асимптота имеет 0 наклон,

высокочастотная асимптота имеет наклон–20 дБ/дек,

асимптоты и сопрягаются на частоте сопряжения .

фазочастотная характеристика на частоте сопряжения принимает значение

при уменьшении частоты относительно частоты сопряжения фазочастотная характеристика стремиться к нулю;

при увеличении частоты относительно частоты сопряжения фазочастотная характеристика стремиться к значению .

Для оценки неизвестных значений параметров K и T по ЛАЧХ необходимо построить низкочастотную асимптоту, имеющую нулевой наклон, и высокочастотную асимптоту, имеющую отрицательный наклон -20 дБ/дек. Точка пересечения этих асимптот дает частоту сопряжения и ординату, соответствующую значению 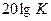, т.е. на частоте значение равно .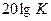

Параметр K находится по формуле .

для определения значения T нужно воспользоваться выражением или , .

Пример расчета асимптотических логарифмических частотных характеристик. Задана передаточная функция инерционного типового звена первого порядка: W (s) =k/ (Ts+1), требуется рассчитать и построить асимптотическую ЛАЧХ.

Решение.

1. Заменим s на jω с учетом того, что и путем несложных преобразований получим: W (jω)= k /(T jω +1)

2. Запишем выражение амплитуды W (ω):

3. Запишем выражение ЛАЧХ L (ω):

Следовательно, в низкочастотной области

Следовательно, в области высокой частоты

4. Частоты, соответствующие точкам сопряжения отрезков, называются сопрягающими и обозначаются ω _с=1/Т

5. Строим график ЛАЧХ:

L (), дБ

Lgk -20дБ\дек

lg

0,1 0,5 ω _с=1/Т 1 2 5 10 100

-10

-20 Низкочастот- Высокочастотная область

ная область