Виды симметрии

В зависимости от того, какие преобразования сохраняют объект ин­вариантным, его симметрию относят к тому или иному виду.

Самые привычные для нас симметрии — геометрические (про­странственные). Именно они чаще всего подразумеваются, когда слово «симметрия» употребляют в обыденном значении. Геометриче­ские симметрии сводятся к инвариантности относительно того или иного геометрического преобразования: поворота вокруг оси, отра­жения в плоскости, инверсии относительно точки и т. д.

Чем больше преобразований оставляет геометрическую фигуру неизменной, тем она более симметрична. Квадрат более симметри­чен, чем прямоугольник, потому что переходит сам в себя при пово­роте не только на 180, но и на 90 градусов в своей плоскости. Кроме того, его диагонали являются осями симметрии, а диагонали прямо­угольника — нет. Самая симметричная фигура — шар (или сфера): любая прямая, проходящая через центр шара, является его осью сим­метрии, любая плоскость, проходящая через центр шара, — плоско­стью симметрии.

Однако симметрии могут быть не только геометрическими.

Важную роль при описании свойств элементарных частиц и дру­гих физических объектов играют калибровочные симметрии — ин­вариантность относительно изменения начала отсчета или масштаба измерения той или иной физической величины. Например, высо­ты всех географических пунктов в нашей стране отсчитываются от уровня Балтийского моря, точнее — от нулевой отметки на футштоке (металлическом стержне) в Кронштадте. Представим себе, что реше­но нулевую отметку перенести на метр выше. При этом абсолютные высоты всех точек, в том числе и гребня плотины Волжской ГЭС, уменьшатся на метр. Однако мощность ГЭС от этого, так же как и от перехода с метров на футы, не изменится.

Еще один вид симметрии — динамические симметрии, сводящие­ся к инвариантности хода того или иного процесса относительно из­менения условий его протекания. Например, известно, что существу­ют электрические заряды двух сортов — положительные и отрица-

2.1. Понятие симметрии и ее значение в естествознании 59

тельные. Представим, что внезапно знак заряда у всех заряженных частиц изменился на противоположный. Повлияет ли это на ход про­цессов в мире? Оказывается, почти нет: атомы из отрицательно заря­женных ядер и положительных электронов (позитронов) останутся такими же стабильными и будут вступать в такие же химические ре­акции; так же будут светить звезды; по-прежнему справедлив будет закон всемирного тяготения...

Симметрии могут быть неполными, или нарушенными. По некото­рым свойствам мир, полученный изменением знаков всех зарядов, будет отличаться от нашего — очень слабо, но все-таки отличаться¹. В качестве другого примера можно привести симметрию человече­ского тела. Правая и левая руки подобны друг другу, но обладают разной функциональностью: 80% людей от рождения правши. Мно­гие непарные органы расположены асимметрично: если не считать редких патологий, сердце находится слева, а печень — справа.

♦•♦ Нарушение симметрии тесно связано с процессами эволюиии, разви­тия, возникновения упорядоченных структур.

На самых первых стадиях развития зародыш любого животного представляет, собой совокупность совершенно одинаковых клеток, возникших в результате деления исходной яйцеклетки, и обладает практически симметрией шара. Однако затем в процессе морфогене­за происходит ряд последовательных нарушений симметрии: возни­кают различия между спинной и брюшной сторонами, головной и хвостовой частями... Высшие животные обладают более низкой сим­метрией строения и функций своего организма, чем древние прими­тивные организмы.

Земля, как и все планеты, в начале своего существования была бесструктурным сгустком вещества. Свойства вещества в центре сгу­стка и на его периферии отличались довольно слабо (п. 5.3). В ре­зультате геологической эволюции Земля приобрела выраженное слоистое строение: земное ядро по составу и свойствам кардинально отличается от земной коры — это очевидное нарушение симметрии. По современным космологическим представлениям (п. 5.1) веще­ство в молодой Вселенной было распределено однородно. Однород­ность означает симметрию относительно пространственных переме-

¹ В физике это обстоятельство известно как нарушение четности в слабых взаимодей­ствиях. Оно было экспериментально установлено By Цзянь-Сюн в 1957 г. (Чет­ность // БСЭ, 3-е изд.).

60 Глава 2. Симметрия природы

2.2. Пространство, время и их симметрии 61

СН

СН

щений: в какую бы точку пространства мы ни перенеслись, плотность и состав вещества в ее окрестностях будут одни и те же. В современ­ной же Вселенной видимое вещество сосредоточено главным обра­зом в звездах; звезды собраны в галактики — огромные звездные ост­рова, состоящие из десятков и сотен миллиардов звезд. Галактики разделены космической пустотой; в межгалактическом пространстве звезд нет. Таким образом, в ходе эволюции Вселенной симметрия од­нородности была утрачена, сохранившись лишь частично: только в масштабах сотен миллионов световых лет и крупнее Вселенную все еще можно считать однородной. В космологии рассматриваются и другие нарушения симметрии в ходе эволюции Вселенной (п. 5.1.5).

2.1.3. Значение симметрии в естествознании

♦♦♦ Исследование симметрии природных объектов и взаимодействий яв­ляется важнейшим методом естественных наук.

Во-первых, это один из способов сведения многообразия окружающе­го мира к ограниченному набору закономерностей. Если мы установи­ли, что любые два электрона принципиально неотличимы, то вместо изучения каждого из бесчисленных электронов в мире можно огра­ничиться изучением свойств любого одного из них. Если мы знаем, что электрон и позитрон симметричны друг другу относительно из­менения знаков зарядов, то мы можем не приводить в справочниках массу и магнитный момент позитрона: они такие же, как у электрона.

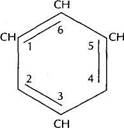
Во-вторых, симметрия свойств объектов отражает симметрию их внутренней структуры. Благодаря этому по внешней форме кристал­ла, например, можно судить о характере расположения атомов в нем и без электронного микроскопа. Другой пример: согласно структур­ной формуле бензола С₆Н₆ (рис. 2.1), предложенной немецким хими­ком Кекуле, в молекуле должны присутствовать три обычных хими­ческих связи С-С и три двойных С=С. Однако как химические, так и физические свойства бензола не согласовывались с гипотезой о су­ществовании в нем разных типов связей углерод-углерод. Это заста­вило признать, что все связи С-С в молекуле бензола полностью симметричны, и разработать соответствующую теорию, которая впо­следствии полностью подтвердилась.

В-третьих, анализ симметрии — один из наиболее мощных эври­стических приемов научного поиска. Специалист часто может дать достаточно полное описание сложной системы или решение сложной задачи, руководствуясь только соображениями симметрии. Для точ-

Рис. 2.1. Структура молекулы бензола

ного описания свойств симметрии разработан изощренный матема­тический аппарат теории групп.

В-четвертых, свойства симметрии объектов и взаимодействий тесно связаны с законами сохранения — важнейшими законами при­роды. Согласно теореме, доказанной в 1918 г. Эмми Нётер,

Г

наличие у системы любой симметрии приводит к сохранению оп­ределенной величины, характеризующей эту систему.

Например, следствием калибровочных симметрии, присущих эле­ментарным частицам и взаимодействиям между ними, является со­хранение числа легких и числа тяжелых частиц (лептонного и барионного заряда) в любой ядерной реакции, сохранение электрическо­го заряда и так далее.