Пример 3. На изготовление 1000 булочек затрачено 5000 изюминок

На изготовление 1000 булочек затрачено 5000 изюминок. Какова вероятность того, что в случайной булочке окажется менее трёх изюминок?

Решение:

Любая изюминка может с равной вероятностью попасть в каждую из 1000 булочек, т.е. вероятность попадания одной изюминки в данную булочку равна 0,001. Можно считать, что производится 5000 испытаний Бернулли, в которых решается вопрос, попадёт ли она в данную булочку. Вероятность «успеха» (попадания) p = 0,001, число испытаний n = 5000, поэтому вероятность того, что в булочке окажется менее 3-х изюминок (т.е. «или 0, или 1, или 2 изюминки») равна:

P(X<3) = P(X=0) + P(X=1) + P(X=2)

P(X<3) =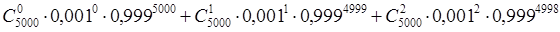

Вычисление искомой вероятности по этой формуле затруднительно. Воспользуемся приближением Пуассона (n – велико, р – мало) при λ = np = 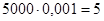, тогда

P(X<3) = P(X=0) + P(X=1) + P(X=2) = .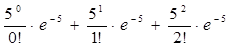

Теперь по таблице распределения Пуассона имеем:

P(X<3) = P(X=0) + P(X=1) + P(X=2) = 0,0067 + 0, 0337 + 0, 0842 = 0,1246

Эти значения подчёркнуты в отрывке таблицы.

Значения функции Пуассона: .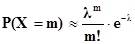

m	l	1,0	2,0	3,0	4,0	5,0	6,0	7,0	8,0	9,0
	0,3679	0,1353	0,0498	0,0183	0,0067	0,0025	0,0009	0,0003	0,0001
	0,3679	0,2707	0,1494	0,0733	0,0337	0,0149	0,0064	0,0027	0,0011
	0,1839	0,2707	0,2240	0,1465	0,0842	0,0446	0,0223	0,0107	0,0050
	0,0613	0,1805	0,2240	0,1954	0,1404	0,0892	0,0521	0,0286	0,0150
	0,0153	0,0902	0,1680	0,1954	0,1755	0,1339	0,0912	0,0572	0,0337

Итак, вероятность того, что в случайной булочке окажется менее трёх изюминок равна 0,1246.

2. Например, если ДСВ Х подчиняется распределению Пуассона, то вероятность того, что Х примет значения от 8 до 12 включительно найдём по формуле

P(8 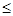X 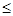12) = P(X=8) + P(X=9) + P(X=10) + P(X=11) + P(X=12).

Теперь опишем ДСВ Х посредством НСВ Y, распределённой нормально с параметрами М(Y) = λ и D(Y) = λ. Тогда искомую вероятность можно будет найти как вероятность попадания нормально распределённой величины в заданный интервал P(7,5<X<12,5). Здесь 0,5 представляет собой поправку на непрерывность, т.к. ДСВ Х=8 в распределении Пуассона аппроксимирована интервалом 7,5 – 8,5 на непрерывной кривой нормального распределения, а ДСВ Х=12 в распределении Пуассона аппроксимирована интервалом 11,5 – 12,5 на непрерывной кривой нормального распределения.

3 вопрос. Производящая функция.

Функция 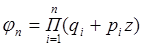, разложение которой по степеням z (где z – произвольный параметр) даёт в качестве коэффициентов вероятности значений СВ Х, называется производящей функцией для этой СВ.

Пример 4.

В билетном зале 3 кассы. Вероятность того, что с 12 часов до 13 они работают, соответственно равны 0.9, 0.8, 0.7. Составьте закон распределения числа работающих касс в течение этого часа, и вычислите числовые характеристики этого распределения.

Решение:

СВ Х – число работающих касс в течение часа – может принимать значения 0, 1, 2, 3.

Вероятности успеха, т.е. того, что каждая из касс работает, по условию равны соответственно р₁ = 0,9; р₂ = 0,8; р₃ = 0,7. Тогда вероятности того, что каждая из касс не будет работать, равны q₁ = 0,1; q₂ = 0,2; q₃ = 0,3.

Распределение СВ Х можно получить через производящую функцию.

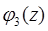= (q₁ + p₁z)(q₂ + p₂z)(q₃ + p₃z) = (0,1 + 0,9z)(0,2 + 0,8z)(0,3 + 0,7z) =

= 0,504z³ + 0,398z² + 0,092z + 0,006.

Каждый из 4-х полученных коэффициентов при z^m (m = 0, 1, 2, 3) в функции 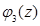выражает соответствующую вероятность P(X=m).

Тогда распределение СВ Х – числа работающих касс – следующее:

Число успехов, X=m (xi)	0	1	2	3
Вероятности, Рn, m (pi)	0,006	0,092	0,398	0,504

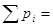0,006 + 0,092 + 0,398 + 0,504 = 1

Найдем числовые характеристики этого распределения:

- Математическое ожидание:

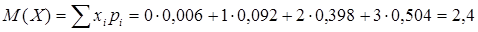кассы.

Т.е. из трёх касс в билетном зале в течение следующего часа будет работать в среднем 2,4 кассы.

- Дисперсия:

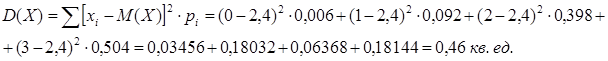
Д/з – решить эту задачу, используя теоремы сложения и умножения вероятностей. Д/з – доказать, что формула Бернулли является частным случаем вычисления вероятностей Рn, m более общего способа через ПФ. См.: 2. Теория статистики с основами теории вероятностей: Учебное пособие для вузов/ И.И. Елисееева, В.С. Князевский, Л.И. Ниворожкина, З.А. Морозова; Под ред. И.И. Елисеевой. – М.: ЮНИТИ-ДАНА, 2001. – С. 111 – 114.

4 вопрос. Гипергеометрическое распределение

ДСВ Х имеет гипергеометрическое распределение, если она принимает значения 0, 1, 2, 3,…, min(n,M) с вероятностями

,

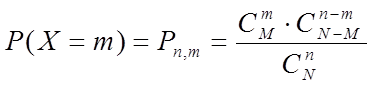Вспомните уже знакомую вам схему невозвращённого шара:

N

М N-M

n

m n-m

Если по формуле вычислить вероятности для всех возможных значений m и поместить их в таблицу, то получим ряд распределения, называемый гипергеометрическим законом распределения.

X=m (x i)	Вероятности, Р(X=m) (p i)
…	…
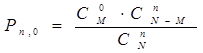
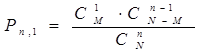
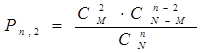
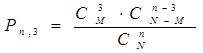
m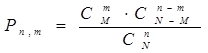
…	…
n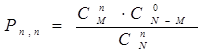
Сумма

Функция распределения F(x):

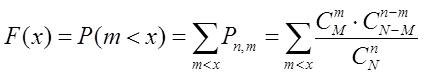
Математическое ожидание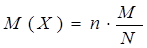

Дисперсия: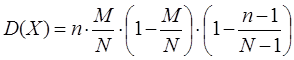

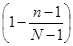- поправка на бесповторность выборки.

Пример 5.

Менеджер по персоналу рассматривает кандидатуры 12 человек, из которых 4 женщины, подавших заявление о приёме на работу в крупную фирму. Будут приняты только 5 человек.

Составьте ряд распределения числа женщин, среди лиц, занявших вакантные должности, и постройте его график.

Найдите числовые характеристики этого распределения.

Запишите функцию распределения и постройте её график.

Чему равна вероятность того, что менее 3-х женщин займут предложенные вакансии?

Решение:

СВ Х - число женщин, среди лиц, занявших вакантные должности – принимает значения 0, 1, 2, 3, 4.

Это - дискретная случайная величина, т.к. ее возможные значения отличаются друг от друга не менее чем на 1, и множество ее возможных значений является счетным.

Очевидно, что отбор кандидатов - бесповторный. Следовательно, испытания - зависимые.

Вышеперечисленные признаки указывают на то, что рассматриваемая случайная величина – число женщин среди лиц, занявших вакантные должности - подчиняется гипергеометрическому закону распределения.

Изобразим ситуацию на схеме:

12 кандидатов

4 женщины 8 мужчин

5 вакансий

0 5

1 4

2 3

3 2

4 1

Составим ряд распределения.

Вычислим вероятности того, что случайная величина примет каждое из своих возможных значений по формуле:

,

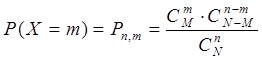По условию задачи N=12, M=4, n=5, m=0, 1, 2, 3, 4

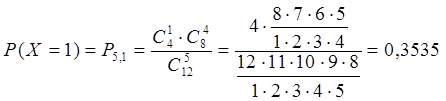
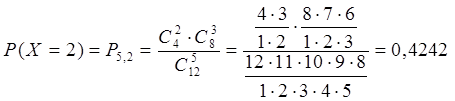
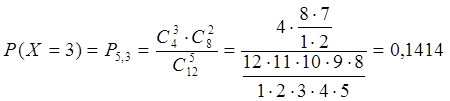
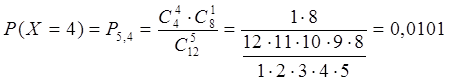
Занесем полученные результаты в таблицу:

Хi	0	1	2	3	4
Рi	0,0707	0,3535	0,4242	0,1414	0,0101

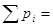0,0707 + 0,3535 + 0,4242 + 0,1414 + 0,0101 = 0,9999» 1.

График полученного распределения вероятностей дискретной случайной величины (полигон распределения вероятностей) изображен на рис 23

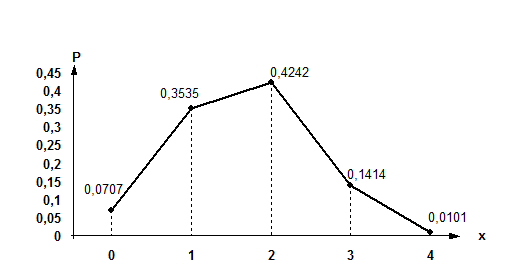
Рисунок 23.

Найдем числовые характеристики данного биномиального распределения: М(Х), D(Х), .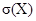

Математическое ожидание определим 2-мя способами:

- как М(Х) ДСВ

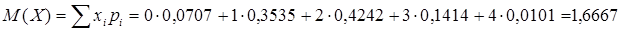
- как М(Х) ДСВ, распределённой по гипергеометрическому закону

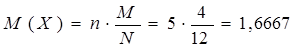женщин

Итак, среди случайно выбранных 5-х кандидатов можно ожидать появление в среднем 1,6667 женщин (точнее, менее двух).

Дисперсию определим:

- как D(X) ДСВ

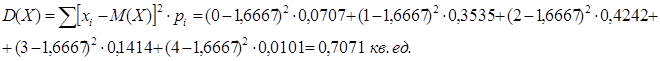
- как D(X) ДСВ, распределённой по гипергеометрическому закону

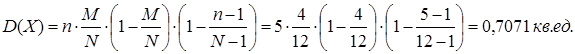
Среднее квадратическое отклонение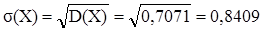

Зададим дискретную случайную величину в виде функции распределения:

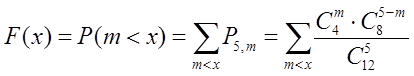
Рассчитаем значения F(х):

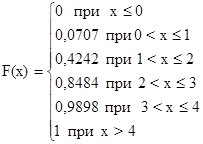
Эти данные можно представить и в виде таблицы:

Х	x £ 0	0 < x £ 1	1 < x £ 2	2 < x £ 3	3 < x £ 4	x > 4
F(x)	0	0,0707	0,4242	0,8484	0,9898	1

График функции распределения вероятностей дискретной случайной величины имеет ступенчатый вид (рис. 24).

Рисунок 24. Функция распределения вероятностей.

Определим вероятность того, что среди 5-х отобранных кандидатов на должности окажется меньше трёхх женщин. «Меньше трёх» - это «или ноль, или одна, или две».

Можно применить теорему сложения вероятностей несовместных событий:

P(X< 3) = P(X = 0) + P(X = 1) + P(X = 2) = 0,0707 + 0,3535 + 0,4242 = 0,8484.