Вопрос. Распределение Пуассона

Дискретная СВ Х имеет закон распределения Пуассона, если она принимает только целые неотрицательные значения 0, 1, 2, …, m, … с вероятностями, вычисленными по формуле Пуассона:

, е – основание натуральных логарифмов (е = 2,71828)

Придавая m целые неотрицательные значения m =0,1,2,3,… можно записать ряд распределения вероятностей, вычисленных по формуле Пуассона.

X=m (x i)	Вероятности, Р(X=m) (p i)
…	…
m
…	…
n
Сумма

+ + + + … + + … + =

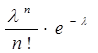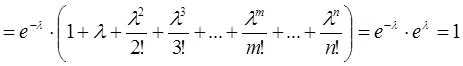
Функция распределения F(x):

,

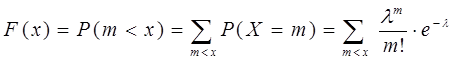Математическое ожидание и дисперсия М(Х) = D(X) = λ

Пример 2.

Начальнику отдела охраны труда и здоровья крупного предприятия обрабатывающей отрасли промышленности поставлена задача проанализировать уровень травматизма работников в производственных коллективах. На этом предприятии в среднем каждые три года имеет место 2 серьёзных несчастных случая. Они происходят случайным образом, и поэтому их нельзя спрогнозировать.

Составить закон распределения числа несчастных случаев, случившихся за три года, и построить его график.

Найти числовые характеристики этого распределения.

Записать функцию распределения числа несчастных случаев и построить её график.

Чему равна вероятность, что за три года произойдёт менее 3-х несчастных случаев?

Решение: Пусть случайная величина Х - число несчастных случаев на предприятии. Все возможные значения случайной величины Х: 0, 1, 2, 3, 4, 5,...

По условию несчастные случай происходят случайно и независимо друг от друга. Следовательно, мы имеем дело с независимыми испытаниями.

Если мы предположим, что вероятность наступления несчастного случая одинакова в любые два периода времени равной длины, и что наступление или ненаступление несчастного случая в любой период времени не зависит от его наступление или ненаступление в любой другой период времени, то последовательность наступлений несчастных случаев может быть описана распределением Пуассона с параметром l = 2.

Вычислим вероятности того, что случайная величина примет каждое из своих возможных значений по формуле Пуассона.:

,

Значение экспоненциальной функции найдём из экспоненциальных таблиц по значению λ. При λ = 2 получаем . Или с помощью встроенной в EXCEL экспоненциальной функции (рис. 9):

Рисунок 9.

Найдем вероятность того, что за три года не произойдёт ни одного несчастного случая:

Аналогично находим и другие вероятности

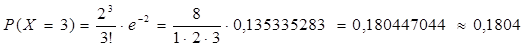
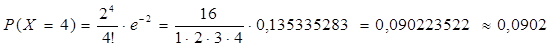
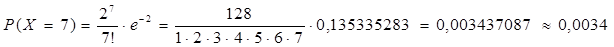
При вероятности, рассчитанные по формуле Пуассона, стремятся к 0.

Получим ряд распределения числа несчастных случаев, случившихся за три года.

Xi	0	1	2	3	4	5	6	7	8	9	10
Рi	0,1353	0,2707	0,2707	0,1804	0,0902	0,0361	0,0120	0,0034	0,0009	0,0002	0,0000

0,1353 + 0,2707 + 0,2707 + 0,1804 + 0,0902 + 0,0361 + 0,0120 + + 0,0034 + 0,0009 + 0,0002 = 0,9999» 1.

СВ можно задать графически многоугольником (полигоном) распределения (рис. 10).

Рисунок 10.

Найдем числовые характеристики полученного распределения случайной величины Х.

Можно рассчитать М(Х), D(Х) и СКО по общим для любой ДСВ формулам.

Математическое ожидание и дисперсия случайной величины, подчиняющейся распределению Пуассона, равны

М(Х) = D(X) = λ = 2

Среднее квадратическое отклонение числа несчастных случаев: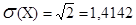

Зададим теперь дискретную случайную величину в виде функции распределения:

Рассчитаем значения F(x):

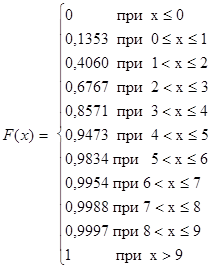
Эти данные можно представить и в виде таблицы:

X	x £0	0<x£1	1<x£2	2<x£3	3<x£4	4<x£5	5<x£6	6<x£7	7<x£8	8<x£9	x > 9
F(х)	0	0,1353	0,4060	0,6767	0,8571	0,9473	0,9834	0,9954	0,9988	0,9997	1

График функции распределения вероятностей дискретной случайной величины имеет ступенчатый вид (рис. 11).

Рисунок 11.

Вероятность того, что за три года произойдёт менее 3-х несчастных случаев (т. е. не более 2-х - «или ноль, или один, или два»), найдём по теореме сложения вероятностей несовместных событий:

Р(Х<3) = P(X£ 2) = P(X=0)+P(X=1)+P(X=2)= 0,1353 + 0,2707 + 0,2707 = 0,6767.