Закон больших чисел в форме Чебышева

Одно из основных утверждений закона больших чисел состоит в том, что значение среднеарифметического 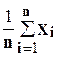случайных величин с равными математическими ожиданиями , при большом n оказывается приближенно равным a:

Будем писать

при ,

если для любого e >0 и достаточно больших n соотношение

(2)

выполняется с вероятностью, стремящейся к 1 с ростом n; запишем это так:

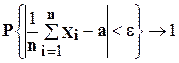при .

это одно из утверждений закона больших чисел. Заметим, что, как и теорема Бернулли, оно не означает, что соотношение (2) достоверно; однако, если n достаточно велико, то вероятность его выполнения близка к 1, например, 0.98 или 0.999, что означает практически достоверно.

Полная формулировка теоремы Чебышева,

Теоремы Чебышева. Если - последовательность попарно независимых случайных величин, имеющих конечные дисперсии, ограниченные одной и той же постоянной:

,

то для любого e>0

при

Задание. Проверить (2) экспериментально для равномерно распределенных слагаемыхна отрезке [0,1].

Если значение e задавать произвольно, а число испытаний выбирать из условия n ³ (9D[X]/e²), то (докажите это) соотношение (2) выполняется с вероятностью P= 0.997, а если n ³ (5.4D[X]/e²) - то с P =0.98.

Положим e₁ = 0.1 и e₂ =0.02, определим два соответствующих значения n₁ =45 и n₂ =1125, и проверим (2) экспериментально (в нашем случае a= 0.5). Выполнение аналогично п.1.