Свойства симметрических матриц

Опред. Матрицу называют симметрической, если a_ij=a_ji. Для всех i,j.

Теорема. Собственные значения симметрической матрицы – действительные числа, собственные векторы – ортогональны.

Док. Ограничимся матрицей размерности 2. Имеем А= 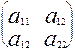. Характеристическое уравнение имеет вид к²-(а₁₁+а₂₂)+(а₁₁а₂₂-а₁₂²)=0. Его дискриминант равен (а₁₁+а₂₂)²-4(а₁₁а₂₂-а₁₂²)= (а₁₁-а₂₂)²+4а₁₂² 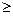0. А это значит – корни квадратного уравнения действительные числа.

Рассмотрим случай разных корней. Тогда по Виету имеем к₁+к₂= а₁₁+а₂₂, и к₁к₂= а₁₁а₂₂-а₁₂² .С другой стороны для к₁ найдем собственный вектор 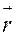₁ из системы Как известно, в этой системе одно из уравнений лишнее, т.к. rancA=1. И потому мы отбросим, например, второе уравнение в системе и возьмем х₂=а₁₁-к₁. Тогда получим собственный вектор 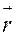₁=(-а₁₂ а₁₁-к₁)^T. Из аналогичных рассуждений найдем 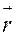₂=(-а₁₂ а₁₁-к₂)^T. Теперь вычислим их скалярное произведение 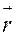_{1 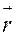2}=а₁₂²+(а₁₁-к₁)(а₁₁-к₂)= а₁₂²+а₁₁²- а₁₁(а₁₁+ а₂₂)+ а₁₁а₂₂-а₁₂² =0.

Если же корни равны, то это происходит только тогда, когда одновременно а₁₂=0 и а₁₁- а₂₂=0. Но это может быть только если к₁= к₂ = а₁₁. Но тогда в качестве 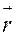₁ можно взять 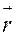₁=(1 0)^T,а в качестве 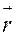₂ можно взять 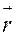₂=(0 1)^T . И все равно они будут ортогональны.