Квадратичные формы и их приведение к каноническому виду

Пусть в ЛП размерности 2 задан 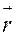=(х1 х2)T в нормированном евклидовом ортогональном базисе i,j.

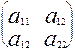
Опред. Выражение ф(х1,х2)= а11х12+2а12 х1 х2 +а22х22=0 где aij - действительные числа, называют квадратичной формой двух переменных х1,х2. Ее можно записать иначе ф(х1,х2)= (а11х1+а12х2) х2+(а12 х1+а22х2)х2. Затем, используя умножение матрицы на вектор получить ф(х1,х2)= =(( 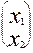), )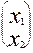=(Ах,х), причем матрица А – симметрическая и, как известно, ее ее собственные векторы ортогональны. Пусть это будут векторы 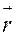1 и 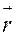2. Тогда их можно нормировать и принять в качестве базисных в ортонормированном евклидовом ЛП. Построим единичные векторы в новом базисе (базисе собственных векторов матрицы А). Получаем и - новые единичные. И в этом новом базисе вектор 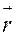=(х’1 х’2)T. Но в этом случае и квадратичная форма примет новый вид ф(х1,х2)= (А(х’1 + х’2 ), х’1 + х’2 ). Но т.к. и - собственные для А, то получаем ф(х1,х2)=((х’1 к1 + х’2 к2 ), х’1 + х’2 )= к1(х’1)2+ к2(х’2)2. Получен новый вид квадратичной формы, в котором отсутствует произведение текущих координат. Такой вид носит название – канонического вида квадратичной формы.

Т.о. в декартовом базисе собственных нормированных векторов матрицы квадратичной формы сама форма принимает канонический вид.

Остается важная задача: установить связь между координатами вектора 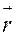=(х1 х2)T начального базиса i,j и координатами того же вектора

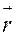=(х’1 х’2)T в новом базисе нормированных собственных векторов матрицы квадратичной формы.

Мы имеем 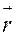= х1i+х2j = х’1I+х’2J. Но I и J тоже векторы, правда единичной длины. И потому I=iCos +jCos(90- ), J= iCos +jCos(90+ ). Или после подстановки полученного вместо координат х’1,х’2 получим связь между старыми и новыми координатами 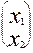= (х’1 х’2)T, которая соответствует матрице поворота плоскости на некоторый угол.