Общий алгоритм решения системы линейных уравнений

Определение. Наибольший из порядков не равных нулю миноров матрицы А называют рангом матрицы и обозначают rankA.

Для поиска ранга используют разные методы. Мы используем метод окаймляющих миноров. Выполним реализацию этого метода на примере.

Пример 1.4. Определить ранг матрицы А= . Решение. Т.к. в матрице есть элементы (“определители” 1-го порядка), не равные нулю, то делаем вывод: . рассмотрим элемент а₁₁=1 и записанный в левом верхнем углу матрицы. Если бы там был записан нуль, то всегда можно переставить местами параллельные ряды матрицы так, чтобы на этом месте был записан ненулевой элемент.

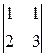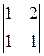Теперь выпишем возможные окаймляющие миноры для элемента а₁₁=1 .Это будут миноры , , , , , . Фактически - эти миноры поставляют “забор”, который оградил данный элемент “пролетами” из частей рядов матрицы. Легко видеть, что уже первый из них не равен нулю. Т.е. . Значит предстоит его окаймлять, тем более, что он записан в левом верхнем углу. Получаем окаймляющие миноры для минора М₂= . Это будут и . Легко подсчитать. что оба они равны нулю. Т.к. других миноров 3-го порядка, окаймляющих минор М₂, нет, то делаем вывод: . При этом М₂ назовем базисным минором матрицы А.

Определение. Матрицу А системы (1) называют основной матрицей системы.

Определение. Если к столбцам основной матрицы приписать справа матрицу-столбец свободных членов, то получится матрица, которую называют расширенная матрица системы.

Так А = основная, а

А₁ = - расширенная матрицы для системы (1).

Теорема Кронекера-Капелли. Для того, чтобы система (1) имела решение (была совместима), необходимо и достаточно, чтобы ранги основной и расширенной матриц были равны. (Без доказательства).

На базе этой теоремы построен алгоритм решения системы линейных уравнений (1):

1-й шаг - выписываем основную А и расширенную А₁ матрицы системы;

2-й шаг - определяем(находим) ранги и ;

3-й шаг - если = , то переходим к шагу 4, иначе делаем вывод, что система не имеет решения (несовместна);

4-й шаг - выписываем базисный минор;

5-й шаг - отбрасываем уравнения, коэффициенты при неизвестных в которых не вошли в базисный минор;

6-й шаг - неизвестные, чьи коэффициенты не вошли в базисный минор, объявляем свободными (считаем известными величинами) и переносим в столбец свободных членов;

7-й шаг - решаем оставшуюся систему, в которой число уравнений равно числу неизвестных и определителем которой является базисный минор, не равный нулю; Метод решения выбираем по необходимости, т.к. система имеет единственное решение;

8-й шаг - записываем решение исходной системы (1).

Пример 1.5. Решите систему, расширенная матрица которой рассмотрена в примере 4, а основная имеет вид А= .

Решение. В данном случае пропущены шаги 1,2,3, т.к установлены ранги основной и расширенной матриц. И эти ранги равны. Поэтому на шаге 4 выписываем готовый базисный минор М₂= . Теперь записываем систему, отбросив третье уравнение и положив свободное переменное х₃=С: . Получаем решение этой системы

Х= . Его принято называть общим, т.к., полагая разные значения С, получим разные решения системы. Теперь запишем решение исходной системы с расширенной матрицей А₁ из примера 4:

Х= . Ответ: система имеет бесчисленное количество решений, определяемых по формуле для Х.