 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Структурный анализ механической части электропривода с помощью частотных характеристик
|
|
Детальный анализ свойств упругих механических систем можно провести на основе двухмассовой расчетной схемы, структура которой представлена на рис. 8.2. Для исследования свойств этой системы как объекта управления примем возмущения M с1= M c2=0 и выполним показанные на рис. 8.3,а…в преобразования ее структуры. Прежде всего, перенесем внутреннюю связь по упругому моменту на выход системы, как показано на рис. 8.3,а.
Эта операция позволяет определить передаточную функцию, связывающую выходную координату со скоростью w1:
 (8.1)
(8.1)

Рис. 8.2. Структурная схема двухмассовой упругой
механической системы без учета внутреннего демпфирования.
Далее находим передаточную функцию двухмассовой системы по управлению при выходной переменной w1. В соответствии со схемой рис. 8.3,б передаточная функция прямого канала:

а обратной связи:

 .
.
Следовательно, искомая передаточная функция с учетом выражения 8.1 определяется так:
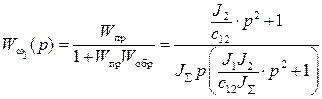 . (8.2)
. (8.2)
Характеристическое уравнение системы:
 .
.
Корни характеристического уравнения:

 (8.3)
(8.3)
где w12 – резонансная частота двухмассовой упругой системы.

Рис. 8.3. Структурные схемы двухмассовой упругой механической
системы без учета внутреннего демпфирования
Для удобства анализа введем следующие обобщенные параметры двухмассовой упругой системы:
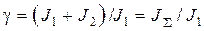 – соотношение масс;
– соотношение масс;
 – резонансная частота системы.
– резонансная частота системы.
С учетом этих обозначений уравнения (8.1) и (8.2) могут быть представлены в виде:
 (8.4)
(8.4)
 (8.5)
(8.5)
Полученные соотношения выражения (8.4) и (8.5) позволяют представить механическую часть электропривода как объект управления в виде трех звеньев, показанных на рис. 8.3,б. С помощью этой схемы нетрудно записать и передаточную функцию системы по управляющему воздействию при выходной переменной w2:
 (8.6)
(8.6)
Передаточной функции формула (8.6) соответствует структурная схема объекта, представленная на рис. 8.3,в. Для анализа свойств системы следует воспользоваться частотным методом теории управления. Уравнение амплитудно-фазовой характеристики (АФХ) получить, подставив в уравнение (8.5) p = jW:
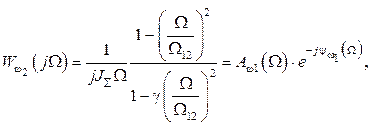 (8.7)
(8.7)
где  – амплитудно-частотная характеристика (АЧХ);
– амплитудно-частотная характеристика (АЧХ);
 – фазо-частотная характеристика (ФЧХ) объекта при выходной переменной w1.
– фазо-частотная характеристика (ФЧХ) объекта при выходной переменной w1.
Соответствующая всем изложенным положениям ЛАЧХ объекта при выходной переменной w1 представлена на рис. 8.4.
Там же построена его ЛФЧХ на основе уравнения АФХ (8.7). В низкочастотной области сдвиг между колебаниями определяется интегрирующим звеном и составляет -90°. При W = W12 /  скачком меняет знак числитель выражения (8.7), что соответствует уменьшению фазового сдвига на 180°. Затем на частоте W = W12, аналогично, изменяется знак знаменателя, и фазовый сдвиг вновь принимает значение -90° в соответствии с высокочастотной асимптотой ЛАЧХ.
скачком меняет знак числитель выражения (8.7), что соответствует уменьшению фазового сдвига на 180°. Затем на частоте W = W12, аналогично, изменяется знак знаменателя, и фазовый сдвиг вновь принимает значение -90° в соответствии с высокочастотной асимптотой ЛАЧХ.

Рис. 8.4. ЛАЧХ двухмассовой упругой системы по
управляющему воздействию при выходной переменной ω1 .
Дата публикования: 2015-10-09; Прочитано: 585 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
