Выбор коэффициента k

Р Д	m	k
0,95	-	1,1
0,99	> 4	1,4
≤ 4	По графику k (l)׀ m на рис. 6.1

Рис. 1. Графики функций k (l)׀ _m

Границы погрешности результата измерения.

В общем случае на погрешность результата измерения с многократными наблюдениями влияют случайные погрешности и неисключенные остатки систематических погрешностей. В этом случае границы погрешности результата измерения 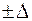оцениваются в порядке, указанном ниже.

1. Пусть 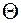- граница НСП (1.16), 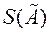- оценка СКО результата измерений (1.4), а 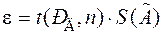- доверительная граница случайной погрешности результата измерения (1.15). Причем оценк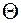и и 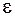выполнены при одинаковой доверительной вероятности .

2. Если 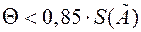, то НСП пренебрегают, считая их несущественными по сравнению со случайными погрешностями, и полагают, что граница погрешности результата измерения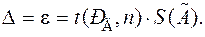

3. При пренебрегают случайной погрешностью по сравнению с неисключенными систематическими погрешностями и полагают, что граница погрешности результата измерения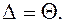

4. В случаях, когда 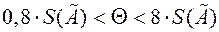границу погрешности результата измерения в метрологии вычисляют путем композиции распределений случайных погрешностей и неисключенных систематических погрешностей, рассматриваемых как случайные величины, по формуле

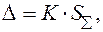(1.17)

где 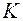- коэффициент, зависящий от соотношения случайной и
неисключённой систематической погрешностей;

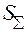- оценка суммарного СКО результата измерения.

Коэффициент 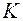вычисляется по формулам

(1.18)

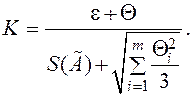(1.19)

Однако выражения (1.17) - (1.19) вызывают у метрологов нарекания, поскольку дают явно заниженные оценки погрешности 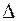. Более правомочным полагают оценивать границу погрешности результата измерения как 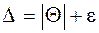, где 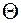- общая граница неисключенных систематических погрешностей (1.16), 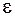- доверительная граница случайной погрешности результата измерения (1.15).

Для рассматриваемых симметричных доверительных границ погрешности результат измерения величины 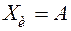должен представляться в следующей форме:

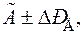(1.20)

где 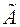- результат измерения (1.1). Числовое значение результата измерения 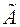должно оканчиваться цифрой того же разряда, что и значение погрешности 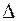. Например, если ,
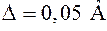то 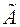= 14,62 В, но не 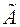= 14,6 В или 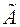= 14,623 В.

Рассмотрим вопрос об ограничении числа n многократных наблюдений. В качестве критерия ограничения n целесообразно использовать указанное выше условие ,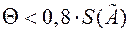
где 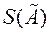- оценка среднеквадратического отклонения результата измерения. Действительно, с ростом n уменьшается 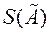, что следует из выражения (1.4). Такое уменьшение целесообразно до достижения равенства . Дальнейшее увеличение числа наблюдений n не имеет смысла, так как при оценке границы погрешности результата измерений случайной погрешностью пренебрегают. 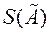Поэтому максимальное число наблюдений n _max можно оценить при подставке в условие выражения для из (6.4)

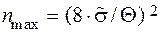, (1.21)

где - оценка СКО наблюдений, вычисляемая по (1.3).