 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Абсолютное значение одного процента прироста
|
|
1 метод
А%09/08=1,1/8,9=0,123 (млн. сом) или 123 тыс. сом в одном проценте прироста
А%;10/09=1,4/10,4=0,134 (млн. сом) или 134 тыс. сом
А% 11/10=1,6/10,8=0,148 (млн. сом) или 148 тыс. сом
А% 12/11=1,4/8,5=0,164(млн. сом) или 164 тыс. сом
2 метод
А%09/08= 0,01*у08=0,01*12,3=0,123
А%10/09=0,01*13,4=0,134
А%11/10=0,01*14,8=0,148
А%12/11=0,01*16,4=0,164
Средний уровень ряда динамики рассчитывается по средней арифметической простой, так как в примере представлен интервальный ряд динамики.
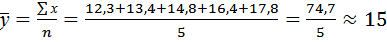 (млн. сом)
(млн. сом)
Средний абсолютный прирост

Или

Средний темп роста
 =
= 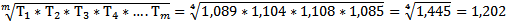
Или
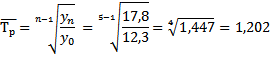
Средний темп прироста
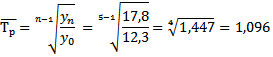
или
 = 109,6%-100%= 9,6%
= 109,6%-100%= 9,6%
Среднее абсолютное содержание одного процента прироста
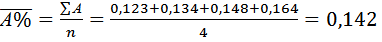 или 142 тыс. сом
или 142 тыс. сом
В одном проценте прироста содержится 142 тыс. сом реализованной продукции прироста.
Пример 8.3. Остатки товарных запасов в торговой точке (тыс. долл.):
- на 1.01.2012г. -22,4
- На 1.04.2012 г. - 23,5
- На 1.07.2012г. -20,8
- На 1.10.2012г. -22,2
- На 1.01.2013 г. -24,6
Определить среднеквартальный остаток товарных запасов.
Решение: Так как нам представлен моментный ряд динамики с равностоящими уровнями среднее значение рассчитаем по средней хронологической взвешенной
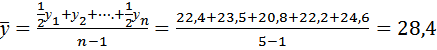 (тыс. долл.)
(тыс. долл.)
Пример 8.4. За октябрь 2012 г. в списочном составе работников предприятия произошли следующие изменения (чел.):
Состояло по списку на 1.10.2012 г.-919
Выбыло с 6.10 - 29
Зачислено с 21.10 - 15
Решение: Имеется моментный ряд динамики с разностоящими уровнями, поэтому среднее значение найдем по формуле средней арифметической взвешенной
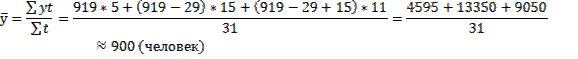
Так как в октябре 31 день, среднесписочная численность работников составила 900 человек.
Пример 8.5. Имеются данные о потреблении овощей по области за 2004-2012 г.г. на одного члена домохозяйства в месяц, кг.
| 10,0 | 10,7 | 12,0 | 10,3 | 12,9 | 16,3 | 15,6 | 17,8 | 18,0 |
Выявить основную тенденцию потребления овощей за 2004-2012 г.г. с помощью трехчленной скользящей средней и аналитического выравнивания по прямой.
Решение. Исчислим трехлетние скользящие средние уровни ряда за 2004-2012 г.г.
За 2004-2006 г.г
 кг;
кг;
За 2005-2007 г.г
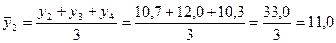 кг и т.д.
кг и т.д.
Результаты расчета трехлетней скользящей средней представим в таблице
Таблица 8.2 Динамика потребления овощей на одного члена домохозяйства за месяц по области за 2004-2012 г.г., кг.
| Годы | Потребление овощей на месяц на одного члена домохозяйства,
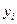
| Скользящие трехлетние суммы
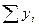
| Трехлетние скользящие средние
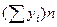
|
| А | |||
10,0 (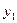 )
10,7 ( )
10,7 (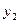 )
12,0 ( )
12,0 (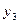 )
10,3……
12,9……
16,3……
15,6……
17,8……
18,0 ( )
10,3……
12,9……
16,3……
15,6……
17,8……
18,0 (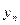 ) )
| -
32,7(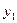 + + 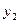 + + 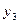 )
33,0 ( )
33,0 (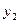 + + 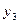 + +  )
35,2…
39,5…
44,8…
49,7…
51,4( )
35,2…
39,5…
44,8…
49,7…
51,4( )
- )
-
| -
10,9 (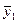 )
11,0 ( )
11,0 (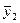 )
11,8…
13,2…
15,9…
16,6…
17,1( )
11,8…
13,2…
15,9…
16,6…
17,1( )
- )
-
|
В результате обработки ряда динамики методом скользящей средней проявилась тенденция к росту потребление овощей.
Для выравнивания ряда динамики по прямой используем уравнение

где 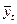 - теоретические уровни;
- теоретические уровни;
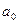 и
и 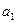 - параметры прямой;
- параметры прямой;
t - показатель времени (дни, месяцы, годы и т.д.).
Таблица 8.3 Исходные и расчетные данные о динамике потребления овощей на месяц на одного члена домохозяйства по области
| Годы | Потребление овощей на месяц на одного члена домохозяйства, у | t |

| yt |
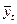
|
| A | 2 | ||||
| 10,0 10,7 12,0 10,3 12,9 16,3 15,6 17,8 18,0 | -4 -3 -2 -1 | -40,0 -32,1 -24,0 -10,3 16,3 31,2 33,4 72,0 | 9,30 10,41 11,52 12,63 13,74 14,85 15,96 17,07 18,18 | ||
| Итого | 123,6 | 66,5 | 123,6 |
Для нахождения параметров 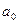 и
и 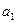 необходимо решить систему нормальных уравнений
необходимо решить систему нормальных уравнений
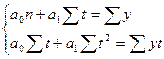
Где у - фактические уровни ряда динамики;
n - число уровней
t – показатель времени, который обозначается порядковыми номерами (например 1, 2, 3, и т.д.).
В рядах динамики техника расчета параметров уравнения может быть упрощена. Для этой цели показатели времени t придают такие значения, чтобы их сумма была равна нулю, т.е.

При этом уравнения системы примут вид:

На основании полученных расчетов можно найти параметры уравнения
 (кг),
(кг),
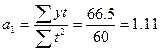 (кг)
(кг)
Уравнение прямой будет иметь вид
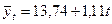
Полученное уравнение показывает динамику роста, т.е. с каждым годом потребление овощей на одного члена домохозяйства возрастало на 1,11 кг.
Подставив в это уравнение значение t получим выравненные теоретические значения 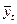 (табл. 8.3, гр. 5).
(табл. 8.3, гр. 5).
После решения уравнения наносим на график фактические уровни и исчисленную прямую линию, характеризующую тенденцию динамического ряда.

Дата публикования: 2015-10-09; Прочитано: 1838 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
