Продолжение таблицы 18

Схема нагружения и законы изменения QY и МХ	Правила
	Если на участке балки: QY > 0, то МХ на этом участке увеличивается слева направо; QY < 0, то МХ уменьшается слева направо; QY = 0, то МХ = const – прямая, параллельная оси.
	Если поперечная сила QY, изменяясь по линейному закону, проходит через нуль, то в сечении, где QY = 0, изгибающий момент МХ достигает максимума или минимума.
	Под сосредоточенной внешней силой F на эпюре QY будет скачок, равный по величине этой силе, а на эпюре МХ в этом месте будет излом.   Под парой сил на эпюре МХ будет скачок, равный по величине моменту пары, а на эпюре QY ничего не изменится.
	На свободном или шарнирно опертом конце балки МХ = 0, если в этом месте не приложена пара сил; а если пара сил приложена, то МХ равен моменту этой пары. QY в этом месте равна внешней сосредоточенной силе или силе реакции.

Подумай и ответь на вопросы

106 Могут ли быть скачки в эпюре изгибающих моментов, если балка нагружена сосредоточенными силами и распределенной нагрузкой?

107 Поперечные силы в сечениях на расстоянии z от концов балки выражены уравнениями

Q_Y1 = -F; Q_Y2 = -F + q · z.

Какими линиями очерчены эпюры этих сил?

108 Изгибающие моменты в сечениях на расстоянии z от концов балки выражены уравнениями

М_Х1 = R_A · z; М_Х2 = М.

Какими линиями очерчены эпюры М_Х?

109 Какой линией очерчена эпюра М_Х, если закон изменения М_Х по длине балки выражается уравнением

?

110 Какая из схем нагружения балки соответствует приведенной эпюре Q_Y (рисунок 162)?

111 Для изображенной балки по эпюре Q_Y определить приложенные к ней силы F₁ и F₂ (рисунок 163).

112 По заданной схеме балки и эпюре М_Х (рисунок 164) определить величину момента М₂.

Рисунок 162 Рисунок 163

113 Укажите схемы тех балок, у которых в сечении 1-1 изгибающий момент равен 0 (рисунок 165).

Рисунок 164 Рисунок 165

Порядок построения эпюр Q_Y и М_Х

1 Найти реакции опор и проверить их. Для жестко защемленной балки их можно не находить, но построение эпюр начинать со свободного конца.

2 Разбиваем брус на участки, границами которых являются сечения, где приложены силы и пары, и где начинается и заканчивается распределенная нагрузка.

3 Нумеруем участки.

4 Применяя метод сечений, определяем:

ü Q_Y = const на участке, если на нем нет распределенной нагрузки (рисунок 166); Рисунок 166

ü Q_Y в начале и конце участка распределенной нагрузки в точках внутри участка (рисунок 167).

5 Строим эпюру Q_Y.

6 Если наклонная Q_Y проходит через нуль (Q_Y = 0), то определяем координату z этого сечения.

Рисунок 167

7 Вычисляем в характерных точках значения М_Х. Причем в точках, где приложены внешние пары сил, изгибающие моменты М_Х определяем левее и правее этой точки (рисунок 168).

8 Строим эпюру М_Х.

9 Определяем максимальную (по модулю) величину М_{Х max} в [Н·мм].

10 Проверяем правильность построения эпюр по правилам контроля эпюр Q_Y и М_Х. Рисунок 168

Построение эпюр Q_Y и М_Х

Пример 24. Построить эпюры Q_Y и М_Х для балки, изображенной на рисунке 169.

Решение.

Так как балка имеет жесткую заделку, то реакции не определяем, но построение эпюр начинаем со свободного конца, откуда проставляем характерные точки А, В, С, D.

Разбиваем брус на участки и нумеруем их, начиная со свободного конца. Применяя метод сечений 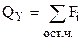, и правило знаков Q_Y (левая часть – со свободного конца) (рисунок 170), вычисляем поперечную силу Q_Y:

Участки I и II (нет распределенной нагрузки).

Q_YI = F = 5 кН (+F, так как слева от сечения вверх).

Q_YII = F = 5 кН.

Участок III (есть распределенная нагрузка).

Рисунок 169

Q_Y определяем в начале ( - правее точки С) и конце ( - левее точки D) участка в точках внутри участка (на расстоянии примерно 0 от точки, например, 1 микрон).

Рисунок 170

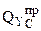= F = 5 кН;

= F – q · 4 = 5 – 2 · 4 = -3 кН.

Сила qz направлена слева от сечения вниз, поэтому со знаком минус.

Строим эпюру Q_Y.

Так как на участке III наклонная Q_Y проходит через нуль в точке К, меняя знак с плюса на минус, то определяем координату Z от точки С:

; .

Вычисляем в характерных точках значения М_Х (рисунок 171):

;

(сила F проходит через точку А и момента относительно этой

точки не дает). Рисунок 171

В точке В приложена внешняя пара сил, поэтому М_Х определяем левее и правее этой точки

;

.

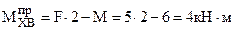В остальных точках:

М_ХС = F · 4 – М = 5 · 4 – 6 = 14 кН·м;

М_ХК = F · (2 + 2 + 2,5) – М – q · 2,5 · = 5 · 6,5 – 6 – 2 · 2,5 · 1,25 ≈ 20 кН·м.

(максимум М_Х на участке III).

М_XD = F · (2 + 2 + 4) – М – q · 4 · 2 = 5 · 8 – 6 – 2 · 8 = 18 кН·м.

Строим эпюру М_Х.

По эпюре М_Х определяем наиболее нагруженное сечение балки, где изгибающий момент М_Х максимален по модулю

М_{Х max} = 20 кН·м = 20 · 10⁶ Н·мм.

Проверяем правильность построения эпюр Q_Y и М_Х по всем правилам контроля и «Правилу лыжника»:

При движении лыжника справа налево по эпюре М_Х,

знак Q_Y показывает настроение лыжника:

ü съезжает с горы – настроение хорошее (+Q_Y) (рисунок 172-а);

ü взбирается в гору – настроение плохое (-Q_Y) (рисунок 172-б);

ü едет по ровной дороге – безразличное настроение (Q_Y = 0) (рисунок 172-в).

а) б) в)

Рисунок 172

Пример 25. Определить поперечную силу, действующую в сечении 1-1 (рисунок 173).

Решение

;

.

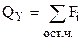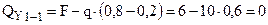Рисунок 173

Пример 26. Определить изгибающий момент в сечении 1-1 (рисунок 174).

Точке А соответствует сечение 1-1 у заделки:

М_ХА = – М + F · (1 + 2 + 2) – q · 2 · (1 + 1) = –2 + 1 · 5 – 2 · 2 · 2 = -5 кН·м.

Рисунок 174

Пример 27. Построить эпюры Q_Y и М_Х для двухопорной балки с консолью (рисунок 175).

Решение. Мысленно отбрасываем опоры А и С и заменяем их силами реакций R_A и R_С. Причем, в шарнирно неподвижной опоре С суммарная реакция R_C = R_CY, так как R_СХ = 0 (нет сил вдоль оси балки).

Определяем реакции опор.

;

Проверка

-1 · 2 -4 – 5 · 2 + 16 = 0;

0 = 0 – реакции определены верно.

Вычисляем Q_Y на участках (слева направо) (смотри рисунок 176):

;

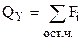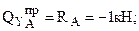
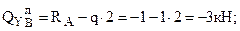
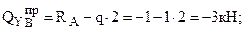
Вычисляем М_Х (смотри рисунок 176):

; ;

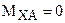Рисунок 176

Рисунок 175

; ;

; Рисунок 177

.

Или справа от сечения (смотри рисунок 177): ;

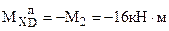; - (нет балки!).

Строим эпюру М_Х. Определяем М_{Х max} = 16 · 10⁶ Н·мм.

Проверяем правильность построения эпюр Q_Y и М_Х по всем правилам контроля эпюр.

114 Определить поперечную силу в сечении 1-1 (рисунок 178).

1) Q_у = 1 кН; 2) Q_у = -7 кН; 3) Q_у = 7 кН.

115 Чему равен изгибающий момент в сечении 1-1 (рисунок 179)?

1) М_{Х 1-1} = 2 кН·м; 2) М_{Х 1-1} = -2 кН·м; 3)М_{Х 1-1} = 3 кН·м.

Рисунок 178 Рисунок 179