Вращательном движении

Пусть тело, которому принадлежат точки А и В, вращается вокруг оси О. За некоторое время t тело повернулось на угол φ, а точки переместились в положение А₁ и В₁ (рисунок 87). Для этих точек:

φ_А = φ_В, ω_А = ω_В, ε_А = ε_В,

но

S_A S_B, S_A > S_B, v_A > v_B.

Пусть r – расстояние от точки А до оси вращения.

Тогда для точки А:

S = r · φ (45)

Продифференцируем выражение (45) по времени:

Рисунок 87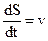

(r вынесем за знак производной, так как для данной точки тела эта величина постоянная).

v = r · ω (46)

Скорость точки вращающегося тела равна произведению угловой скорости тела на расстояние от точки до оси.

Чем дальше точка находится от оси, тем больше ее скорость, например, для схемы (рисунок 87) получим

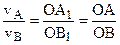
Продифференцируем по времени формулу (46)

;

Получим

(47)

Ускорения а_t и ε направлены в одну сторону.

Нормальное ускорение точки

;

(48)

Полное ускорение точки

(49)