Канонические уравнения метода сил

Для определения неизвестных силовых факторов в эквивалентной системе составляются уравнения, выражающие равенство нулю перемещений по направлениям лишних неизвестных в так называемой канонической форме, что свидетельствует о том, что они составляются по определенному закону (канону).

Рассмотрим один раз статически неопределимую систему (рис. 6а). В ней снято ограничение на вертикальное перемещение точки С, которое может быть вызвано как заданными нагрузками так неизвестной силой Х ₁. Полное перемещение точки С по направлению Х ₁:

.

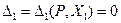На основании принципа независимости действия сил перемещения, вызванные одновременным приложением нескольких сил, равны сумме перемещений от приложения каждой силы в отдельности, т.е.

, (2)

где – перемещение точки приложения неизвестной силы Х ₁ направлению ее действия, вызванное действием Х ₁;

- – перемещение по направлению силы Х ₁, вызванное заданными нагрузками Р,m,q.

Для линейно-деформируемых систем между перемещениями и вызвавшей их силой справедливо равенство

(3)

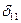где - перемещение точки приложения силы Х ₁ по направлению действия неизвестной , вызванное единичной силой Можно сказать иначе: - перемещение , отнесенное к Х ₁ т.е. и рассматривать его как часть перемещения 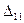, приходящуюся на единицу усилия Х ₁. Соответственно не совпадают размерности и названия и 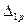: - коэффициент канонического уравнения, 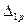- свободный член канонического уравнения.

С учетом (3) уравнение (2) примет вид

.

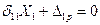Это каноническая форма уравнения перемещений для один раз статически неопределимой системы.

Для системы с двумя “лишними“ связями (рис.6б) уравнения перемещений сечений в точке С имеют вид

где - взаимное перемещение смежных сечений в т.С по направлению Х ₁ от заданной нагрузки и неизвестных сил Х ₁, Х ₂;

- - взаимное перемещение смежных сечений в т.С по направлению Х ₂ от тех же нагрузок.

С учетом принципа независимости действия сил

(4)

где - полное взаимное перемещение сечения, к которому приложено усилие Х ₁ по направлению Х ₁ от всех заданных и всех неизвестных сил;

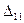- - частное перемещение сечения, к которому приложено усилие Х ₁, по направлению Х ₁ от усилия Х ₁;

- - частное перемещение сечения, к которому приложено усилие Х ₁, по направлению Х ₁ от усилия Х ₂;

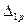- - частное перемещение сечения, к которому приложено усилие Х ₁, по направлению Х ₁ от всех заданных нагрузок;

- - полное взаимное перемещение сечения, к которому приложено усилие Х ₂ по направлению Х ₂ от всех заданных и всех неизвестных сил;

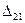- - частное перемещение сечения, к которому приложено усилие Х ₂, по направлению Х ₂ от усилия Х ₁ и так далее.

Первый индекс указывает сечение и направление его перемещения, второй – причину, вызывающую это перемещение.

Переписав уравнения (4) с использованием канонических коэффициентов получим

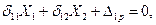
Это каноническая форма уравнений метода сил для дважды статически неопределимой системы.

По аналогии можно записать в канонической форме уравнения для “ n ” раз статически неопределимой системы:

---------------------------------------------- (5)

-----------------------------------------------

Число уравнений всегда равно степени статической неопределимости n.

Форма записи канонических уравнений не зависит от геометрии системы и вида нагружения, но их физический смысл может быть различным. Например, для эквивалентной системы (рис. 6б) они означают, что взаимные вертикальные и горизонтальные линейные перемещения в точке С отсутствуют, а для эквивалентной системы (рис.6а) те же уравнения фиксируют равенство нулю абсолютного линейного (вертикального) перемещения в точке С.