 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Задание 4. Вычислить приближенно значения определенных интегралов, взяв три члена разложения подынтегральной функции в ряд; указать погрешность
|
|
1. 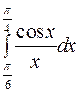
| 2. 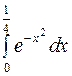
|
3. 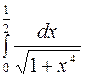
| 4. 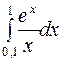
|
5. 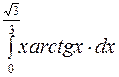
| 6. 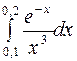
|
7. 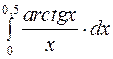
| 8. 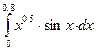
|
9. 
| 10. 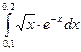
|
11. 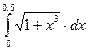
| 12. 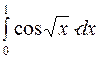
|
13. 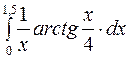
| 14. 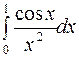
|
15. 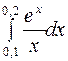
| 16. 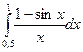
|
17. 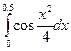
| 18. 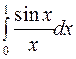
|
19. 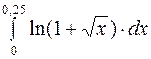
| 20. 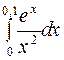
|
Задание 5. Найти разложение в степенной ряд решения 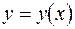 дифференциального уравнения
дифференциального уравнения 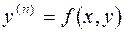 , удовлетворяющего начальному условию
, удовлетворяющего начальному условию 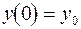 .
.
1. 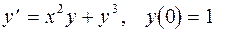
2. 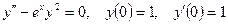
3. 
4. 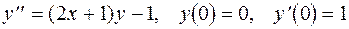
5. 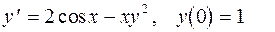
6. 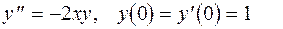
7. 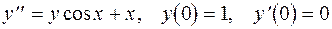
8. 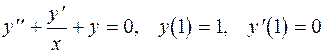
9. 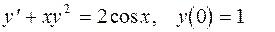
10. 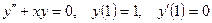
11. 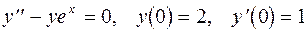
12. 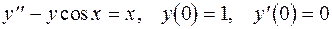
13. 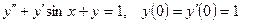
14. 
15. 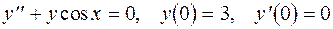
16. 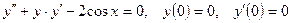
17. 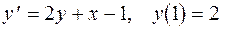
18. 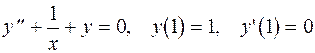
19. 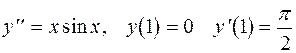
20. 
Контрольная работа №1 по теме
"Векторная алгебра и аналитическая геометрия"
Вариант №1
1.Выяснить образуют ли векторы 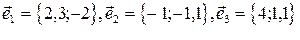 базис? Если да, то разложить по нему вектор
базис? Если да, то разложить по нему вектор 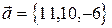 .
.
2. Найти вектор 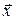 , зная, что он параллелен вектору
, зная, что он параллелен вектору
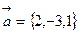 и удовлетворяет условию
и удовлетворяет условию 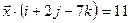 .
.
3. Записать каноническое уравнение кривой 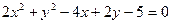
и сделать чертеж.
4. Дан треугольник с вершинами в точках А(1,1), В(-2,3), С(4,7). Написать уравнение медианы, проведенной из вершины А.
Вариант №2
1. Выяснить, образуют ли векторы 
базис? Если да, разложить по нему вектор 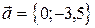 .
.
2. Вектор 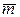 параллелен вектору a={2,-1, 3}, образует острый угол с осью OX. Зная, что
параллелен вектору a={2,-1, 3}, образует острый угол с осью OX. Зная, что 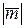 =14, найти его координаты.
=14, найти его координаты.
3. Записать каноническое уравнение кривой и сделать чертеж.
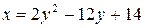
4. Найти отрезки, отсекаемые на координатных осях плоскостью проходящей через точки А(3,1,1); В(1,4,1); С(1,1,7).
Вариант №3
1. Вектор 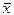 коллинеарен вектору
коллинеарен вектору 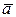 ={6;-8;-7,5}, образует острый угол с
={6;-8;-7,5}, образует острый угол с
осью OZ. Зная, что ½ 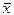 ½=50, найти его координаты.
½=50, найти его координаты.
2. Выяснить, образуют ли векторы 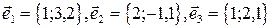
базис? Если да, разложить по нему вектор 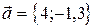 .
.
3. Дан треугольник с вершинами в точках А(1,1), В(-2,3), С(4,7). Написать уравнение медианы, проведенной из вершины В.
4. Найти точку пересечения прямой 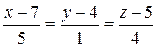
и плоскости 3x-y+2z-5=0.
Вариант №4
1. Найти вектор х, коллинеарный вектору 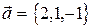 и удовлетворяющий условию
и удовлетворяющий условию 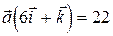 .
.
2. Выяснить, образуют ли векторы 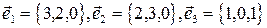
базис? Если да, разложить по нему вектор 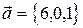 .
.
3. Построить линию, определяемую уравнением:
2x2 + 4y2 - 8x + 16y - 1 = 0.
4.Дан треугольник с вершинами в точках А(1,1), В(-2,3), С(4,7). Написать уравнение высоты, проведенной из вершины С.
Вариант №5
1. Вектор 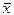 , перпендикулярный к векторам
, перпендикулярный к векторам 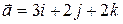 и
и 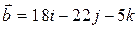 образует с осью ОУ тупой угол. Найти координаты вектора
образует с осью ОУ тупой угол. Найти координаты вектора 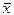 , зная, что ½
, зная, что ½ 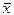 ½=14.
½=14.
2. Если векторы 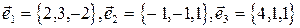 образуют базис, то разложите по нему вектор
образуют базис, то разложите по нему вектор 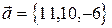 .
.
3. Найти уравнение прямой, проходящей через точки А(2,-1,4) и В(3,2,-1)
4. Построить линию, определяемую уравнением:
2x2 + 4y2 - 16 = 0.
Вариант №6
1. Найти вектор 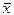 , зная, что он перпендикулярен к векторам
, зная, что он перпендикулярен к векторам 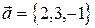 и
и 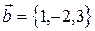 и удовлетворяет условию
и удовлетворяет условию 
2. Выяснить, образуют ли векторы 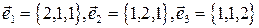 базис? Если да, разложить по нему вектор
базис? Если да, разложить по нему вектор 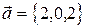 .
.
3. Построить линию, определяемую уравнением:
2x2 - 4y2 + 16y = 0.
4. Составить уравнение прямой, проходящей через ось абсцисс и точку
А(3,-2).
Вариант №7
1. Дан вектор: 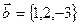 . Найти вектор
. Найти вектор 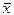 , параллельный оси OZ и удовлетворяющий условиям
, параллельный оси OZ и удовлетворяющий условиям 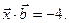
2. Выяснить, образуют ли векторы 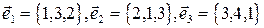
базис? Если да, разложить по нему вектор 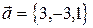 .
.
3. Написать уравнение прямой, проходящей через точки А(1,1) и В(3,2).
4. Найти точку пересечения прямой 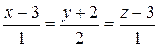 и плоскости
и плоскости
x+y+z-5=0.
Вариант №8
1. Дан вектор: 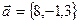 . Найти вектор
. Найти вектор 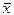 , параллельный оси OХ и удовлетворяющий условию
, параллельный оси OХ и удовлетворяющий условию 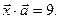
2. Выяснить, образуют ли векторы 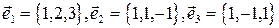
базис? Если да, разложить по нему вектор 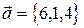 .
.
3.. Построить линию, определяемую уравнением:
x2 + y2 - 8x + 16y - 1 = 0.
4.Найти объем тетраэдра, ограниченного координатными плоскостями и плоскостями 2x-y+z-12-0.
Вариант №9
1. Выяснить, образуют ли векторы 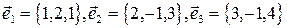
базис? Если да, разложить по нему вектор 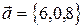 .
.
2. Построить линию, определяемую уравнением:
2x2 + 4y2 - 8x + 16y - 1 = 0.
3. Составить уравнение перпендикуляра, опущенного из точки М(2,3,-5) на плоскость 4x-2y+5z-12=0.
4. Выяснить, принадлежат ли точки А(-1,2), В(3,4), С(1,2) одной прямой.
Вариант №10
1.. Записать каноническое уравнение кривой 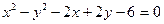 .
.
Сделать чертеж.
2. Выяснить, образуют ли векторы 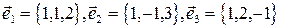
базис? Если да, разложить по нему вектор 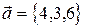 .
.
3. Найти объем параллелепипеда, построенного на векторах
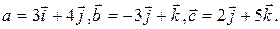
4. Найти расстояние от точки А(1,2,1) до плоскости 2x-2y+z+6=0.
Вариант №11
1. Найти вектор х, если он параллелен 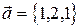 и удовлетворяет условию
и удовлетворяет условию 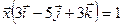 .
.
2. Выяснить, образуют ли векторы 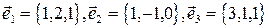
базис? Если да, разложить по нему вектор 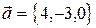 .
.
3. Найти расстояние от точки К(1,2,3) до плоскости 2x-2y+z+6=0.
4. Записать каноническое уравнение кривой 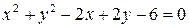 .
.
Сделать чертеж.
Вариант №12
1. Найти вектор х, удовлетворяющий условиям 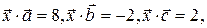 если
если 
2. Выяснить, образуют ли векторы 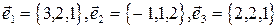
базис? Если да, разложить по нему вектор 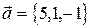 .
.
3. Вычислить высоту параллелограмма, построенного на векторах
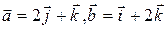 .
.
4. Записать каноническое уравнение этой кривой и построить кривую, заданную уравнением 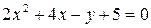 .
.
Вариант №13
1. Записать каноническое уравнение кривой 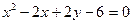 .
.
Сделать чертеж.
2. Выяснить, образуют ли векторы 
базис? Если да, разложить по нему вектор 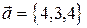 .
.
3.Вычислить объем параллелепипеда, построенного на векторах

4. Дан треугольник с вершинами в точках А(-1,2), В(0,1) и С(1,4). Написать уравнение медианы, проходящей через вершину А.
.
Вариант №14
1. Выяснить, образуют ли векторы 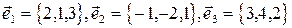
базис? Если да, разложить по нему вектор 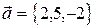 .
.
2. Найти угол между прямой 2х+3у-1=0 и прямой, проходящей через точки М1(-1,2), М2 (0,3).
3.Найти уравнение плоскости, проходящей через точку А(1,2,3), перпендикулярно оси OZ.
4. Записать каноническое уравнение кривой 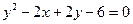 . Сделать чертеж.
. Сделать чертеж.
Вариант №15
1. Записать каноническое уравнение кривой 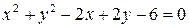 .
.
Сделать чертеж.
2. Выяснить, образуют ли векторы 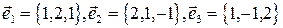
базис? Если да, разложить по нему вектор 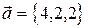 .
.
3. Определить углы, образованные вектором 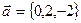 c координатными осями.
c координатными осями.
4. Найти угловой коэффициент и отрезок, отсекаемый на оси ординат прямой, проходящей через точки А(1,2) и В(-3,1).
Вариант №16
1. Найти вектор 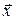 , коллинеарный вектору
, коллинеарный вектору  и удовлетворяющий условию
и удовлетворяющий условию 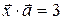 .
.
2. Выяснить, образуют ли векторы 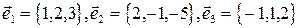
базис? Если да, разложить по нему вектор 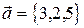 .
.
3. Определить объем параллелепипеда, построенного на векторах
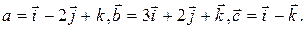
4. Записать каноническое уравнение и построить кривую 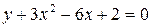 .
.
Вариант №17
1. Найти уравнение прямой, проходящей через точку М(-1,3) и точку пересечения прямых 2х-у-1=0, 3х+у-4=0.
2. Выяснить, образуют ли векторы 
базис? Если да, разложить по нему вектор  .
.
3. Записать каноническое уравнение кривой 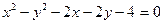 .
.
Сделать чертеж.
4. Найти отрезки, отсекаемые на координатных осях плоскостью, проходящей через точки А(3,1,1), В(1,4,1), С(1,1,7).
Вариант №18
1. Найти уравнение прямой, проходящей через точку А(1,-1) параллельно прямой, соединяющей точки М1(2,-3), М2 (5,1).
2. Выяснить, образуют ли векторы 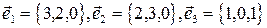
базис? Если да, разложить по нему вектор 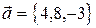 .
.
3. Известны вершины пирамиды А(0,0,0), И(3,2,-1), С(2,3,2),
Д(4,0,-3). Вычислить объем пирамиды и высоту.
4. Записать каноническое уравнение и построить линию
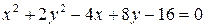 .
.
Вариант №19
1. Дан треугольник с вершинами в точках А(1,5), В(-4,3), С(2,9). Найти уравнение высоты, проведенной из вершины А.
2. Выяснить, образуют ли векторы 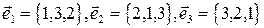
базис? Если да, разложить по нему вектор 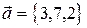 .
.
3. Составить уравнение плоскости, параллельной плоскости 3x-6y+4z-12=0, и проходящей через точку А(4,6,5).
4. Составить уравнение прямой, проходящей через точки А(-2,8,7) и В(6,8,9).
Вариант №20
1. Написать уравнение прямой, проходящей через точку М(4,3) перпендикулярно к вектору 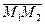 , если М1(0,-2), М2 (3,5).
, если М1(0,-2), М2 (3,5).
2. Выяснить, образуют ли векторы 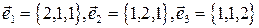
базис? Если да, разложить по нему вектор  .
.
3. Найти расстояние от точки А(1,2,2) до плоскости 2x-3y+4z+12=0.
4.Записать каноническое уравнение и построить кривую 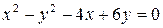 .
.
Дата публикования: 2015-10-09; Прочитано: 986 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
