D.1. Коэффициент отражения от нагрузки

В разд. 3 были рассмотрены собственные электромагнитные волны в регулярных линиях передачи (ЛП) бесконечной длины.

Рассмотрим конечный отрезок ЛП, включённый между источником электромагнитных волн (генератором) и оконечным устройством (нагрузкой). Генератор в общем случае возбуждает в ЛП весь спектр собственных волн с разными амплитудами.

Пусть поперечный размеры ЛП и рабочая частота таковы, что в ней может распространяться только основной тип волны. Включение нагрузки на конце ЛП приводит к появлению в ЛП кроме волны бегущей к нагрузке (падающей волны) дополнительной отраженной волны, распространяющейся от нагрузки к генератору (рис. D.1).

В дальнейшем будем считать ради простоты, что ЛП не имеет потерь и что в ней основным типом волны является поперечная электромагнитная волна, т.е. волна класса Т. Как отмечалось в разд. 3, к таким относятся все ЛП, которые содержат как минимум два изолированных проводника: коаксиальный кабель; двухпроводная и многопроводная линии; полосковые линии и др. Рассмотрение других ЛП проводится аналогично.

В дальнейшем под U _пад и U _отр будем понимать напряжения падающей и отражённой волны в ЛП. Отметим, что при рассмотрении ЛП с волнами классов Е, Н и Е (Н) под U _пад и U _отр можно понимать проекции векторов 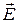падающей и отражённой волн на плоскость, перпендикулярную оси линии передачи.

В дальнейшем будем полагать, что начало системы координат находится в месте расположения нагрузки, а ось системы координат направлена от нагрузки к генератору.

Рисунок D.1 – Линия передачи конечной длины

Из материалов разд. 3 следует, что выражения для комплексных амплитуд напряжений падающей и отражённой волн имеют следующий вид:

, (D.1)

, (D.2)

где – амплитуда напряжения падающей волны; – постоянная распространения волны или продольное волновое число; – длина волны в линии передачи.

Величина в формуле (D.2) называется комплексным коэффициентом отражения от нагрузки. Из формул (D.1) и (D.2) видно, что она равна отношению комплексных амплитуд напряжений отражённой и падающей волн на нагрузке, которая, как уже отмечалось, находится в сечении лини , т.е.

, (D.3)

где – модуль коэффициента отражения, – его аргумент коэффициента отражения.

Из определения следует, что комплексный коэффициент отражения характеризует степень согласования линии с нагрузкой, т.е. «способность» нагрузки поглощать мощность подающей волны. При этом модуль коэффициента отражения определяет амплитуду отраженной волны, а аргумент – скачок фазы при отражении (разность фаз падающей и отраженной волны на нагрузке).

Умножая формулы (D.1) и (D.2) на и отделяя в полученном произведении действительную часть, получаем следующие формулы:

, (D.4)

. (D.5)

Из теории ЛП конечной длины известно, что комплексный коэффициент отражения может быть вычислен по известным значениям волнового сопротивления линии и сопротивления нагрузки по следующей формуле:

. (D.6)

Волновым сопротивлением линии называют отношение амплитуд напряжения и тока в бегущей волне.