С.11. Объемные резонаторы

Простейшим электромагнитным резонатором является колебательный LC -контур. В этом контуре запас электрической энергии создаётся в конденса­торе, а запас магнитной энергии – в катушке индуктивности. Переход энергии от электрического поля к магнитному сопровождается пространственным пере­мещением энергии из конденсатора в индуктивность. Уже в метровом диапа­зоне волн контур перестаёт работать удовлетворительно: сказываются межвит­ковые ёмкости катушек, индуктивность выводов и пластин конденсатора.

В диапазоне дециметровых и более коротких волн применяются резонаторы, в которых электромагнитные колебания возникают внутри ограниченного объёма, поэтому их называют объёмными резонаторами. Различают следующие типы объемных резонаторов:

- квазистационарные резонаторы, это резонаторы, в объёме которых можно выделить области, где в основном сосредоточены электрическая или магнитная энергия;

- резонаторы бегущей волны, представляющие собой отрезок направляющей системы, свёрнутый в кольцо;

- резонаторы из закороченных отрезков направляющих систем;

- открытые резонаторы, используемые преимущественно в оптическом диапазоне и представляющие собой систему из двух противостоящих зеркал.

С.11.1. Собственные и вынужденные колебания в резонаторах

Собственные колебания возникают в резонаторе при внешнем им­пульсном воздействии, когда в него поступает порция энергии. После про­цесса установления, колебания в резонаторе становятся квазигармоническими затухающими. При этом любой вектор электромагнитного поля в резонаторе зависит от времени по следующему закону:

,

где – вектор, зависящий только от пространственных координат и определяющий структуру поля колебаний в резонаторе; – собственная круговая частота колебаний резонатора; – собственная добротность резонатора.

У объемного резонатора существует бесконечное число собственных колебаний (в отличии от обычного колебательного LC -контура), каждому из которых соответствует определенная структура электромагнитного поля и определенные значения и . Основным типом колебаний (на практике используется обычно этот тип колебаний) называется колебание с наименьшей резонансной частотой.

Вынужденные колебания обусловлены внешними периодическими воздействиями, при этом энергия в резонатор поступает каждый период. Если частота этих колебаний совпадает с одной из резонансных частот резонатора, возникает резонанс, сопровождающийся резким увеличением амплитуды колебаний. Линия связи от внешнего источника доставляет в резонатор только небольшое количество энергии, необходимое для восполнения потерь резонатора.

С.11.2. Параметры резонаторов в режиме вынужденных колебаний

1. Резонансная частота () или резонансная длина волны , которая связана с собственной частотой следующей формулой

.

2. Собственная добротность , которую можно определить как

,

где – средняя за период энергия, запасённая в резонаторе; – средняя за период мощность потерь в резонаторе.

В теории LC -контуров собственная добротность определяется как отношение ( – индуктивность катушки контура) к сопротивлению потерь в контуре.

Собственная добротность определяется через потери в проводящей оболочке резонатора и диэлектрике с помощью следующих формул:

,

где , .

При расчете собственной добротности не учитываются потери во внешних цепях резонатора (). Для учета этих потерь вводят понятие нагруженной добротности резонатора, которая определяется по следующей формуле:

,

где величину

,

называют внешней добротностью резонатора.

3. Резонансная характеристика – зависимость комплексного входного сопротивления резонатора от частоты. Величина комплексного входного сопротивления резонатора зависит как от конструкции резонатора, так и от конструкции элемента связи резонатора с направляющей системой. Модуль и аргумент комплексного входного сопротивления резонатора определяют амплитудно-частотную и соответственно фазочастотную характеристики резонатора.

4. Полоса пропускания резонатора определяется обычно из условия, что внутри полосы пропускания амплитудно-частотная характеристика не изменяется более чем в раза, при этом .

5. Структура электромагнитного поля резонатора, которая определяет поведение векторов электромагнитного поля внутри резонатора. Сведения о структуре поля резонатора позволяют оптимальным способом соединить резонатор с генератором и нагрузкой.

С.11.3. Квазистационарные резонаторы

К квазистационарным резонаторам относят тороидальный, магнетронный и коаксиальный резонатор с зазором.

На рис. С.12 изображен тороидальный резонатор, ис­пользуемый в клистронах. В нем электрическое поле сосредоточено почти пол­ностью в зазоре шириной , а магнитное – в тороидальной области. Резонансная частота основного колебания воздуш­ного тороидального резона­тора рассчитывается по следующей формуле:

.

На рис. С.13 изображен магнетронный резонатор, используемый в магнетронах – генераторах СВЧ боль­шой мощности и сос­тоящий из 8 ячеек. В каждой ячейке электрическое поле в основном сосредото­чено в узком зазоре шириной , магнитное поле – в цилинд­рической полости радиуса . Резонанс­ная частота основного колеба­ния ячейки воздушного магнетронного ре­зонатора рассчитывается по следующей формуле:

.

На рис. С.14 изображен коаксиальный резонатор с зазором, используемый на длинах волн более 1 метра. В зазоре шириной (между пластинкой и закорачивающей стенкой кабеля) сосредоточено, в основном, электрическое поле, в остальном объеме – как электрическое, так и магнитное поле. Резонансная частота основного колебания воздушного коаксиального резонатора находится из следующего трансцендентного уравнения:

,

где 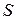– площадь пластинки.

Рисунок С.14 – Коаксиальный резонатор с зазором

С.11.4. Резонаторы из закороченных отрезков направляющих систем

Как уже отмечалось, объёмные резонаторы из закороченных отрезков направляющих систем, в отличие от обычных колебательных контуров, характеризуются бесконечным числом собственных колебаний. Основным типом колебаний (на практике используется обычно этот тип колебаний) называется колебание с наименьшей резонансной частотой. Каждый тип колебаний характеризуется своей структурой поля, соответствующей структуре поля собственных волн. Основной тип колебаний соответствует основному типу волны в направляющей системе. Рассмотрим некоторые типы резонаторов из закороченных отрезков направляющих систем.

Коаксиальный резонатор представляет собой отрезок коаксиального волновода длиной , закороченный с обоих концов проводящими пластинами. Основное колебание этого резонатора называется Т колебанием, так как оно соответствует волне типа Т в коаксиальном кабеле. Коаксиальные резонаторы широко применяются в качестве волномеров, колебательных контуров в радиопередающих устройствах, в фильтрах и др.

Резонансная длина волны основного колебания коаксиального резонатора определяется формулой

.

Структура поля основного колебания представлены на рис. С.15.

Собственная добротность Т колебания определяется формулой

,

где активная часть поверхност­ного сопротивления металлических сте­нок резонатора.

Как показывают численные расчеты у коаксиальных резона­торов из меди собственная доб­ротность на волнах до 10 см может достигать нескольких тысяч и быстро падает по мере умень­шения резонансной длины волны.

Прямоугольный резонатор представляет собой закороченный с двух сторон отрезок прямоугольного волновода длиной . Основным типом колебаний в этом резонаторе является колебание *), его резонансная частота и собственная добротность определяются следующими формулами:

, .

Структура поля основно­го колебания представлены на рис. С.16.

Как показывают числен­ные расчеты у прямоугольных резонаторов с колебанием Н₁₀₁ собственная добротность на волнах сантиметрового диапа­зона может достигать несколь­ких десятков тысяч единиц.

Цилиндрический резона­тор представляет собой зако­роченный с двух сторон отре­зок круглого волновода. Если длина отрезка больше ра­диуса волновода, то основным типом колебаний в этом резонаторе является колебание , если , то – колебание . Собственная добротность цилиндрических резонаторов с колебанием достигает в сантиметро­вом диапазоне нескольких со­тен тысяч единиц. Это позво­ляет использовать их в качест­ве высокоточного волномера.

Резонансная длина волны колебаний в цилиндрических резонаторах с колебаниями и колебаниями определяется по следующим формулам:

, .

Собственная добротность резонаторов, заполненных диэлектриком без потерь, определяется по следующим формулам:

для колебания

;

для колебания

;

для колебания

.

Структура поля колебаний , и представлены соответственно на рис. С.17, рис. С.18 и рис. С.19.

Рисунок С.19 – Структура поля колебания

цилиндрического резонатора