Законы Снеллиуса. Коэффициенты Френеля

При рассмотрении вопросов распространения электромагнитных волн в случае наличия Земли и атмосферы необходимо учитывать явления, которые происходят при падении плоских волн на границу раздела двух сред; при дифракции волн; при распространении волн в неоднородной среде и пр.

Рассмотрим вначале явления происходящие при падении плоских волн на плоскую границу раздела двух сред. Пусть границей раздела является плос­кость YOZ, которая разделяет две среды с различными параметрами (рис. 5.1). Пусть на границу раздела падает плоская волна под углом j. Выясним, какие волновые процессы происходят на границе раздела (плоскость YOZ).

Эту задачу удобно (и наиболее просто) рассматривать отдельно для двух случаев поляризации, когда у падающей волны вектор 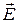перпенди­кулярен плоскости падения (нормально поляризованная волна) и когда у падающей волны вектор перпендикулярен плоскости падения (параллельно поляризованная волна). Плоскостью падения называется плоскость, проходящая через нормаль к границе раздела и направление распространения волны (в рассматриваемом случае плоскость XOZ является плоскостью падения).

Представим электромагнитное поле в первой среде в виде суммы падающей и отраженной плоской волны, а во второй – в виде преломленной плоской волны.

В случае нормальной поляризации комплексные амплитуды вектора 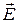падающей, отражённой и преломлённой волн представим в следующем виде:

, (5.1)

, (5.2)

, (5.3)

где , и – углы падения, отражения и преломления; и – коэффициенты отражения и преломления нормально поляризованной волны; и – комплексные (в общем случае) волновые числа первой и второй среды соответственно.

Из формул (5.1) – (5.3) видно, что коэффициенты и можно определить следующим образом. Коэффициентом отражения (преломления) для нормально поляризованной волны называется величина, равная отношению комплексной амплитуды вектора 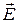отраженной (преломленной) и комплексной амплитуды вектора 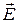падающей волны на границе раздела.

Отметим, что комплексные амплитуды векторов , соответствующие комплексным амплитудам, определяемым соотношениями (5.1) … (5.3), легко найти, используя второе уравнение Максвелла для комплексных амплитуд, которое имеет следующий вид (см. соотношения (1.36)):

. (5.4)

В случае параллельной поляризации комплексные амплитуды вектора падающей, отражённой и преломлённой волн представим в следующем виде:

, (5.5)

, (5.6)

. (5.7)

где и – коэффициенты отражения и преломления параллельно поляризо­ванной волны.

Из формул (5.5) … (5.7) видно, что коэффициенты и можно определить следующим образом. Коэффициентом отражения (преломления) для параллельно поляризованной волны называется величина, равная отношению комплексной амплитуды вектора отраженной (преломленной) и комплексной амплитуды вектора падающей волны на границе раздела.

Отметим, что комплексные амплитуды векторов 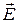, соответствующие комплексным амплитудам, определяемым соотношениями (5.5) … (5.7), легко найти, используя первое уравнение Максвелла для комплексных амплитуд, которое имеет следующий вид (см. соотношения (1.36)):

. (5.8)

Величины , , и , входящие в соотношения (5.1) … (5.3) и
(5.5) … (5.7) называются коэффициентами Френеля.

Используя граничные условия (1.22) и формулы (5.1) … (5.8) нетрудно получить следующие выражения для определения неизвестных нам величин, входящих в формулы (5.1) … (5.7) (углы отражения и преломления и коэффициенты Френеля). Эти выражения имеют следующий вид:

j₁ = j, (5.9)

, (5.10)

, (5.11)

, (5.12)

, (5.13)

, (5.14)

где и – комплексные (в общем случае) волновые сопротивления первой и второй среды соответственно,

. (5.15)

Равенства (5.9) и (5.10) при действительных и (обе среды без потерь) называют первым и вторым законами Снеллиуса.

Из формул (5.11) … (5.14) видно, что коэффициенты Френеля в общем случае являются комплексными величинами и зависят как от параметров обеих сред, так и длины волны (если хотя бы одна из сред имеет потери). В следующих разделах будет проведен анализ коэффициентов Френеля для некоторых практически важных случаев.

Пусть на границу раздела падает волна круговой или эллиптической по­ляризации. В этом случае падающую волну целесообразно представить в виде суперпозиции двух волн, одна из которых поляризована нормально, другая – параллельно. Определяя для каждой из этих волн коэффициенты отражения и преломления (по формулам (5.11) … (5.14)) легко определить параметры отраженной и преломленной волн.

Рассмотрим случай, когда вторая среда является анизотропной средой, и когда вол­новые числа второй среды различны для нор­мально и параллельно поляризованных волн. Пусть на границу раздела падает вол­на, представимая в виде суммы нормально и параллельно поляризованных волн. Выясним, что будет происходить с этой волной на гра­нице раздела. Из законов Снеллиуса следует, что в первой среде появиться отраженная вол­на, а во второй среде возникнуть две волны, идущие в различных направлениях (рис 5.2). Этот факт называется явлением двойного лучепреломления. В теории распространения волн в ионосфере одну из этих волн называю обыкновенной волной, другую необыкновенной.

Отметим, что коэффициенты Френеля, определяемые формулами
(5.11) … (5.14), в большинстве практически важных случаев можно использовать при расчетах коэффициентов отражения (преломления) от поверхности Земли.