Электромагнитного поля

Уравнения Максвелла являются линейными дифференциальными уравнениями в частных производных с постоянными коэффициентами. Пусть сторонние источники электромагнитного поля являются гармоническими. Очевидно, что и возбужденные ими поля также будут гармоническим, т.е. могут быть записаны в виде (1.26). Как отмечалось в предыдущем параграфе в этом случае вместо действительных векторов вида (1.26) можно использовать комплексные векторы вида (1.27).

Получим уравнения, связывающие между собой комплексные векторы электромагнитного поля для случая линейной изотропной среды. Для этого рассмотрим систему уравнений электродинамики в дифференциальной форме

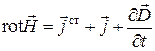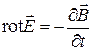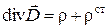, , , (1.30)

совместно с материальными уравнениями

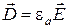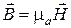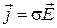, , . (1.31)

Пусть среда является однородной. Подставим материальные уравнения (1.31) в уравнения Максвелла (1.30). Тогда получим следующие уравнения:

, , , .

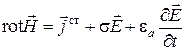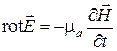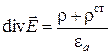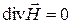Подставим в последние уравнения следующие равенства:

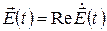, . (1.32)

Учитывая формулу (1.29) и тот факт, что операцию Re можно вынести за знак операторов rot и div, получаем следующие соотношения:

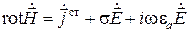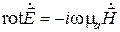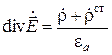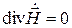, , , . (1.33)

Соотношения (1.33) являются уравнениями Максвелла для комплексных векторов электромагнитного поля. Так как 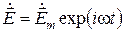, а 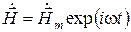, то в уравнениях (1.33) величину 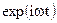можно сократить. В этом случае получим, что комплексные амплитуды векторов электромагнитного поля, т. е. величины также удовлетворяют уравнениям (1.33). Отметим, что уравнения вида (1.33) в литературе часто называют уравнениями Максвелла в комплексной форме.

Нетрудно показать, что четвертое уравнение системы (1.33) является следствием второго уравнения, а третье (для среды без потерь) – первого. В этом случае система уравнений Максвелла сводится к двум уравнениям:

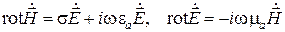(1.34)

для комплексных векторов или

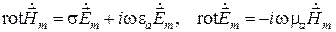(1.35)

для комплексных амплитуд векторов электромагнитного поля.