Завдання 5. Виконати інтегрування раціональної функції

Виконати інтегрування раціональної функції

У вищій алгебрі доводиться наступна теорема: Якщо раціональна функція має степінь многочлена в чисельнику менший степеня многочлена в знаменнику і многочлен представлений у вигляді ,

то таку функцію можна записати так:

(1)

і 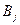- деякі дійсні числа. Для визначення цих чисел діють з тих міркувань,що многочлени в правій і лівій частинах рівності після зведення до спільного знаменника мають бути тотожно рівні. Прирівнюючи коефіцієнти при однакових степенях х, одержують систему рівнянь для визначення невідомих і .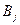

Приклад 5.1

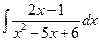, де

Розкладемо раціональну підінтегральну функцію на елементарні дроби за формулою (1)

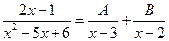
Множимо обидві частини рівняння на і одержуємо

або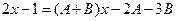

Прирівнюємо коефіцієнти при однакових степенях х та одержуємо систему рівнянь першого степеня відносно А і В

, звідки 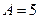, . Отже,

Обчислюємо заданий інтеграл

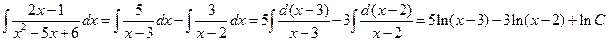
Відповідь:

Приклад 5.2

Розкладемо раціональну підінтегральну функцію на елементарні дроби за формулою (1)

Помноживши обидві частини рівняння на , одержимо вираз

У останньому виразі розкриваємо дужки та групуємо доданки

Прирівнюємо коефіцієнти лівої і правої частин рівняння при , , , і та одержуємо систему

; Розв’язок системи: , , , , .

Отже розкладання має вигляд

Обчислюємо заданий інтеграл

Тема: Поняття числового ряду, його сума та збіжність