Исследование и решение систем линейных алгебраических уравнений методом Гаусса

Рассмотрим систему линейных алгебраических уравнений, при этом число неизвестных и число уравнений в системе могут быть любыми числами. Очевидно, что если эти числа не совпадают, то решить систему с помощью обратной матрицы или при помощи формул Крамера не представляется возможным.

В этом случае для решения системы может быть применен универсальный метод решения любой системы линейных алгебраических уравнений – метод Гаусса.

Для некоторых систем не требуется находить решение, а требуется лишь провести исследование системы, т.е. выяснить, имеет ли данная система решения и, если имеет, то сколько. Ответ на эти вопросы можно получить с помощью нового понятия – понятия ранга матрицы.

Ранг матрицы и его применение при исследовании систем линейных

алгебраических уравнений

Рассмотрим систему m линейных алгебраических уравнений с n неизвестными (2.1):

,

Как известно, система может иметь единственное решение, может иметь множество решений и, наконец, может не иметь решения. Ответ на вопрос о существовании и количестве решений дает теорема Кронекера-Капелли. Прежде чем сформулировать эту теорему введем понятие ранга матрицы.

Рассмотрим матрицу А размерности m x n. Ранее было дано понятие минора элемента квадратной матрицы. Дадим более общее понятие минора определенного порядка для матрицы А.

Минором порядка r матрицы А называется определитель, составленный из любых r строк и любых r столбцов матрицы А.

Для квадратной матрицы порядка n минором (n -1) порядка будет любой определитель, полученный из А вычеркиванием какой-нибудь строки и какого-либо столбца.

Минором порядка (n -2) будет любой определитель матрицы, полученный из А вычеркиванием двух любых строк и двух любых столбцов и т.д. Минором второго порядка будет определитель, составленный из любых двух строк и любых двух столбцов матрицы А, а минором первого порядка будет любой элемент матрицы А.

Например, для А = минором третьего порядка будет определитель этой матрицы; одним из миноров второго порядка будет ; минором первого порядка будет любой из элементов матрицы.

Итак, для квадратной матрицы порядка n наибольший порядок минора будет равен также n.

Для прямоугольной матрицы размерности m x n наибольший порядок минора будет равен наименьшему из чисел m и n.

Например, для матрицы А = порядка 2х3 можно составить минор, у которого наибольший порядок будет равен 2, т.е. наименьшему из чисел 2 и 3.

Для дальнейшего нам понадобятся миноры, которые не равны нулю. Совершенно очевидно, что если для какой-то матрицы все миноры r –го порядка равны нулю, то и все миноры порядка (r +1) также будут равны нулю.

Рангом матрицы А называется наибольший порядок минора, отличного от нуля. Обозначение: rang A.

Если применять только определение, то нахождение ранга матрицы должно сводиться к следующему.

Вначале из матрицы А составляются миноры наибольшего возможного порядка, например, порядка n, если n < m. Если хотя бы один из этих миноров не равен нулю, то rang A = n. В противном случае, составляются миноры порядка n -1 и выясняется существует ли среди них хотя бы один ненулевой. Если да, то rang A = n -1, если нет, то составляются миноры порядка n -2 и т.д.

Очевидно, что такой процесс является достаточно трудоемким и, по сути, не нужным, так как существует особый метод нахождения ранга матрицы. Этот метод состоит в выполнении преобразований над матрицами, которые не меняют ее ранг.

Элементарными преобразованиями матриц назовем следующие преобразования:

Отбрасывание нулевой строки (столбца).

Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.

Изменение порядка строк (столбцов) матрицы.

Прибавление к каждому элементу одной строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на любое число.

Транспонирование матрицы.

Теорема 2.3. Ранг матрицы не изменяется при элементарных преобразованиях.

Доказательство теоремы следует из того, что при элементарных преобразованиях элементы строк или столбцов складываются, вычитаются, умножаются на числа или просто переставляются. Все эти действия по свойствам определителей не изменят наивысший порядок отличных от нуля миноров исходной матрицы.

С помощью элементарных преобразований можно привести квадратную матрицу к треугольному или прямоугольную матрицу к, так называемому, ступенчатому виду. Ранги таких матриц находятся очень просто.

1. Рассмотрим квадратную матрицу А треугольного вида, т.е.

.

Применяя несколько раз формулу разложения определителя по элементам последней строки получим | А | = а ₁₁× а ₂₂× …. а _nn.

Итак, для матрицы треугольного вида определитель равен произведению диагональных элементов, а ранг такой матрицы равен количеству ненулевых элементов, стоящих на главной диагонали.

2. Рассмотрим прямоугольную матрицу А. Назовем ее ступенчатой матрицей, если она имеет вид

,

где а_ii ¹ 0, i = 1,2, …, r; r £ n.

Замечание. Условие r £ n всегда может быть достигнуто транспонированием матрицы.

Очевидно, что ранг ступенчатой матрицы равен r, так как имеется минор r –го порядка, отличный от нуля.

Итак, для того чтобы найти ранг произвольной матрицы А нужно с помощью элементарных преобразований свести ее к треугольному или ступенчатому виду и определить ранг полученной матрицы.

Рассмотрим пример.

Пример 2.6. Найти ранг матрицы

А = .

Решение. Преобразуем матрицу, используя элементарные преобразования: поменяем первую и вторую строки местами; к каждому элементу третьей строки прибавим соответствующий элемент полученной первой строки, умноженной на 2; к каждому элементу четвертой строки прибавим соответствующий элемент полученной первой строки. После преобразований получим

~> ~> ~>

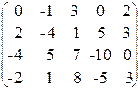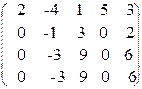К каждому элементу третьей строки прибавить соответствующие элементы второй строки, умноженные на -3. Аналогично поступаем с элементами четвертой строки. Затем убираем нулевые строки. Получим

~> ~> .

Последняя матрица имеет ступенчатый вид и содержит миноры второго порядка, отличные от нуля, следовательно, ее ранг равен 2, но тогда и ранг исходной матрицы также равен 2.

Понятие ранга существенно используется при исследовании систем линейных алгебраических уравнений вида (2.1). Напомним, что основной матрицей системы А называется матрица, составленная из коэффициентов при неизвестных. Введем понятие расширенной матрицы системы.

Расширенной матрицей системы называется матрица, состоящая из основной матрицы с присоединенным к ней столбцом свободных членов, т.е.

.

Теорема Кронекера-Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу расширенной матрицы этой системы.

Теорема Кронекера-Капелли может быть дополнена следующим утверждением.

Утверждение 2.1 .

1. Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение.

2. Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесконечное множество решений.

Теорему и утверждение можно записать в более компактной форме.

Для системы (2.1) справедливо:

1. Если rang A = rang C = n, то система имеет единственное решение.

2. Если rang A = rang C < n, то система имеет множество решений.

3. Если rang A < rang C, то система не имеет решений.

Очевидно, что неравенство rang A > rang C не может быть выполнено никогда, так как матрица А является частью матрицы С.

Перейдем к рассмотрению еще одного метода решения системы линейных алгебраических уравнений – методу Гаусса.

Метод Гаусса решения систем уравнений

Метод Гаусса – метод последовательного исключения неизвестных – заключается в том, что с помощью элементарных преобразований расширенную матрицу системы приводят к треугольному или ступенчатому виду, затем по полученной матрице восстанавливают систему, по которой и судят о том, имеет ли она решения и какие. В случае, когда среди уравнений преобразованной системы есть противоречивые уравнения, система решений не имеет. В случае, когда такого уравнения нет, система имеет либо единственное решение (если число уравнений равно числу неизвестных), либо имеет множество решений (когда число уравнений меньше числа неизвестных). Решения последовательно находятся из восстановленной системы.

Достоинства метода Гаусса по сравнению с другими методами состоят в следующем:

метод менее трудоемкий;

позволяет решать систему с любым числом неизвестных и уравнений;

позволяет однозначно установить, совместна система или нет, а в случае совместности найти ее решения – единственное или бесконечное множество.

Рассмотрим применение метода Гаусса при решении трех систем.

Пример 2.7. Решить систему методом Гаусса

.

Решение. Запишем расширенную матрицу системы, имеем

~> ~> ~> .

По полученной матрице системы восстановим саму систему, получим

.

Решаем ее снизу вверх. Из последнего уравнения х ₃ = 2. Подставляя это значение во второе уравнение, найдем х ₂ = 3. Затем, подставляя эти два найденных значения в первое уравнение, получим х = -1.

Система имеет единственное решение х = -1, х ₂ = 3, х ₃ = 2.

Пример 2.8. Решить систему методом Гаусса

Решение. Запишем расширенную матрицу системы, имеем

~> ~> .

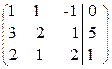По полученной матрице системы восстановим саму систему, получим

.

Последнее уравнение системы противоречиво, так как является неверным равенством, следовательно, данная система несовместна.

Система решений не имеет.

Пример 2.9. Решить систему методом Гаусса

.

Решение. Запишем расширенную матрицу системы, имеем

~> ~> ~> .

По полученной матрице системы восстановим саму систему, получим

.

Эта система состоит из двух уравнений с тремя переменными. Выразим какие-нибудь две переменные через третью, например, х ₁ и х ₂ через х ₃, получим

=> .

Система имеет бесчисленное множество решений, которые связаны формулой 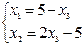, где переменная х ₃ может принимать любое значение от -¥ до + ¥.

Ответ: , х ₃ – любое число.

Итак, применяя метод Гаусса к системе (2.1) можно получить либо единственное решение системы, либо формулы, определяющие бесконечную совокупность решений, либо, наконец, можно доказать, что система решений не имеет.

Все рассмотренные ранее понятия, а именно, понятия матрицы, определителя, ранга, обратной матрицы, системы линейных алгебраических уравнений, а также приведенные методы решения этих систем находят широкое применение при рассмотрении различных экономических вопросов. В частности, система линейных алгебраических уравнений и ее решение с помощью обратной матрицы является главной частью в модели межотраслевого баланса (модели Леонтьева).