 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Симплекс-метод розв’язування задачі лінійного програмування
|
|
Для розв’язування задачі лінійного програмування застосовують симплекс-метод. Для цього необхідно, щоб задача лінійного програмування (2.3), (2.4) мала канонічний вигляд, тобто якщо в кожному i -му рівнянні рівностей з (2.4) міститься змінна така  , що коефіцієнт перед нею 1, в той же час коефіцієнти перед такою ж змінною у інших рівняннях дорівнюють 0 (така змінна присутня лише в одному рівнянні та називається базисною). Також у випадку, коли b 1³0, …, bm ³0, задача лінійного програмування має допустимий канонічний вигляд.
, що коефіцієнт перед нею 1, в той же час коефіцієнти перед такою ж змінною у інших рівняннях дорівнюють 0 (така змінна присутня лише в одному рівнянні та називається базисною). Також у випадку, коли b 1³0, …, bm ³0, задача лінійного програмування має допустимий канонічний вигляд.
Якщо задача не записана у канонічному вигляді, то це можна зробити шляхом введення необхідної кількості штучних змінних в рівняння (2.4); у функцію мети штучна функція входить з коефіцієнтом 0.
Якщо задача лінійного програмування записана у канонічному вигляді, то функцію мети записують таким чином, щоб виключити з неї базисні змінні, залишивши небазисні, які називаються вільними. Розглянемо це на прикладі.
Приклад. Записати задачу лінійного програмування у канонічному вигляді:
Q (x)=2 x 1+3 x 2+5 x 3+8 x 4+3 x 5®min
 x 1–3 x 2+ 4 x 4 =6,
x 1–3 x 2+ 4 x 4 =6,
x 2+ x 3+2 x 4 =8,
– x 2+ x 4+ x 5=2,
xi ³0.
Підкреслимо базисні змінні та перетворимо функцію мети, виключивши з неї базисні змінні. Це можна зробити, віднявши від неї перше рівняння, домножене на 2 (коефіцієнт при першій базисній невідомій), друге, домножене на 5 та третє, домножене на 3. Функція мети тоді набуде вигляду
Q (x)=7 x 2-13 x 4+58.
Після такого запису задача лінійного програмування може бути записана у вигляді симплекс-таблиці. Для наведеного прикладу запишемо симплекс-таблицю (Рис. 2.3).

Рис. 2.3. Симплекс-таблиця та її основні елементи.
Цій таблиці відповідає вершина многогранника допустимої області з координатами x 1=6, x 3=8, x 5=2 (вільні члени, які відповідають базисним змінним), x 2=0, x 4=0 (нулі для вільних змінних).
Симплекс-метод розв’язування задачі лінійного програмування полягає у виконанні таких правил:
1. Вибираємо ведучий стовпчик. Таким стовпчиком буде найменший з тих, у яких pj <0. Нехай таким буде стовпчик з номером j*.
2. Вибираємо ведучу стрічку. Якщо всі aij* £0, то мінімуму не існує (функція мети необмежена знизу в допустимій області). Якщо не всі aij* £0, тоді для додатних aij* знаходимо  . Тоді ведучою стрічкою буде стрічка з номером i*, для якої обчислене відношення буде мінімальним.
. Тоді ведучою стрічкою буде стрічка з номером i*, для якої обчислене відношення буде мінімальним.
Таким чином, знайдено ведучий елемент ai*j*.
3. Замінюємо базис з допомогою ведучого елементу: базисна змінна xi* в результаті цього стає вільною, а вільна змінна xj* - базисною.
В результаті симплекс-таблиця буде змінюватися за наступними правилами (елементи нової таблиці будемо позначати символом “^”):
1) Замінюємо базисну і вільну змінні  ,
,  (міняються місцями базисна та вільна змінні),
(міняються місцями базисна та вільна змінні),  ,
,  (інші змінні залишаються на місці).
(інші змінні залишаються на місці).
2) Знаходимо нові значення ведучого елемента:  (ведучий елемент залишається на місці та замінюється на обернений).
(ведучий елемент залишається на місці та замінюється на обернений).
3) Знаходимо нові значення ведучого стовпчика:  , i¹i*,
, i¹i*,  (кожен елемент ведучого стовпчика ділиться на ведучий елемент з протилежним знаком).
(кожен елемент ведучого стовпчика ділиться на ведучий елемент з протилежним знаком).
4) Знаходимо нові значення ведучої стрічки:  , j¹j*,
, j¹j*, 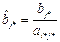 (кожен елемент ведучої стрічки ділиться на ведучий елемент).
(кожен елемент ведучої стрічки ділиться на ведучий елемент).
5) Знаходимо нові значення інших елементів симплекс-таблиці: 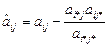 , i¹i*, j¹j*,
, i¹i*, j¹j*,  , j¹j* (у новому стовпчику записується різниця елемента старого стовпчика та добутку елемента ведучого стовпчика та ведучої стрічки, поділеного на ведучий елемент (Рис. 2.4)).
, j¹j* (у новому стовпчику записується різниця елемента старого стовпчика та добутку елемента ведучого стовпчика та ведучої стрічки, поділеного на ведучий елемент (Рис. 2.4)).
6) Знаходимо нові значення стовпчика вільних членів (аналогічно до 5)): 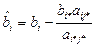 , i¹i*,
, i¹i*,  .
.
В результаті переходу до нової симплекс-таблиці повинні виконуватися нерівності:  ,
,  .
.

| j | j* | |||||
| i | aij | --- | aij* | |||
| | | | | |||||
| i* | ai*j | --- | ai*j* | |||
| j | j* | |||||
| i | 
| --- | 
| |||
| | | | | |||||
| i* | 
| --- | 
| |||
Рис. 2.4. Модифікація симплекс-таблиці.
Приклад. Знайти розв’язок задачі лінійного програмування симплекс-методом.
x 1 + x 2 +3 x 5 = 1,
– x 3 + x 4 = 2,
2 x 1 + 2 x 3 + x 6 = 6,
– x 1 + 3 x 3 –3 x 5 + x 7 = 4,
x 1³0, …, x 7³0,
 Q (x)=2 x 1-3 x 3+2 x 5+32®min.
Q (x)=2 x 1-3 x 3+2 x 5+32®min.
Ця задача має канонічний вигляд. Виділимо базисні змінні та запишемо симплекс-таблицю (Рис. 2.5).
| -1 | |||||
| 6:2 | |||||
| -1 | -3 | 4:3 | |||
| -3 | -32 |
Рис. 2.5.
1) Знайдемо ведучий стовпчик. Це стовпчик з індексом j =3, оскільки у ньому елемент p 3=–3<0.
2) Знайдемо ведучу стрічку. У ведучому стовпчику є два додатні елементи: a 63=2, a 73=3. Для вибору знайдемо мінімум часток  та
та  . Оскільки остання частка менша, тому ведучим елементом буде a 73=3.
. Оскільки остання частка менша, тому ведучим елементом буде a 73=3.
3) Проведемо заміну базису, для цього:
а) у новій таблиці замінимо індекси (замість стовпчика 3 буде стовпчик 7, замість рядка 7 буде рядок 3);
б) замінимо ведучий елемент оберненим  ;
;
в) замінимо елементи ведучого стовпчика, для чого поділимо кожен з елементів стовпчика на ведучий, з протилежним знаком (поділимо на –3);
г) замінимо елементи ведучої стрічки, для чого поділимо кожен з її елементів на ведучий (поділимо на 3) (Рис. 2.6);

| ||||
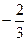
| ||||

| 
| -1 | 
| |
Рис. 2.6.
д) Знайдемо решту елементів нової симплекс-таблиці. Наприклад, елемент  (Рис. 2.4, 2.5). Аналогічно знаходимо інші елементи (Рис. 2.7).
(Рис. 2.4, 2.5). Аналогічно знаходимо інші елементи (Рис. 2.7).
| 1:3 | |||||

| 
| -1 | 
| ||

| 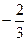
| 
|  :2 :2
| ||

| 
| -1 | 
| ||
| -1 | -28 |
Рис. 2.7.
Як бачимо, одержана симплекс-таблиця не є остаточною (елемент p 5=–1<0). Тому повторимо для неї пошук ведучого елемента. Одержимо наступну таблицю (рис. 2.8).

| 
| 
| |||
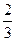
| 
| 
| 
| ||
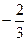
| 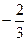
| 
| |||

| 
| 
| |||

| 
| -27 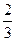
|
Рис. 2.8.
У одержаній таблиці всі pj >0, тому процес завершений. Розв’язком задачі лінійного програмування буде точка з координатами x 1=0, x 2=0, x 3=  , x 4=
, x 4=  , x 5=
, x 5=  , x 6=
, x 6=  , x 7=0. В цій точці функція мети буде набувати значення Q 0=27
, x 7=0. В цій точці функція мети буде набувати значення Q 0=27 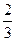 .
.
2.1.4. Двоїста задача
Для кожної задачі лінійного програмування можна поставити двоїсту задачу, яка пов’язана з початковою таким чином, що вільні члени початкової задачі стають коефіцієнтами функції мети і навпаки, матриця системи нерівностей транспонується, нерівності міняються на протилежні, а функцію мети потрібно максимізувати. Це видно з формул (2.7) – (2.10).
Початкова задача:
Q (x)= p 1 x 1+…+ pnxn ®min (2.7)
a 11 x 1+ a 12 x 2+…+ a 1 n xn ³ b 1,
a 21 x 1+ a 22 x 2+…+ a 2 n xn ³ b 2, (2.8)
…
am 1 x 1+ am 2 x 2+…+ amnxn ³ bm,
x 1³0, x 2³0, …, xn ³0.
Двоїста задача:
G (u)= b 1 u 1+…+ bmum ®max (2.9)
a 11 u 1+ a 21 u 2+…+ am 1 um £ p 1,
a 12 u 1+ a 22 u 2+…+ am2um £ p 2, (2.10)
…
a 1 nu 1+ a2nu 2+…+ amnum £ pn,
u 1³0, u 2³0, …, um ³0.
Розглянемо без доведення теореми двоїстості.
Теорема 1. Якщо розглянути задачу, двоїсту до двоїстої задачі, то одержимо початкову задачу.
Теорема 2. Якщо в одній із задач допустима область порожня, то в двоїстій функція мети необмежена знизу (при знаходженні мінімуму) чи зверху (при знаходженні максимуму).
Теорема 3. Якщо існує розв’язок задачі лінійного програмування, то існує розв’язок і двоїстої до неї, а оптимальні значення функцій мети однакові:
G (u)£max G =min Q £ Q (x).
Остання теорема може застосовуватися для розв’язку задач лінійного програмування. Щоб знайти розв’язок конкретної задачі, можна перейти до двоїстої, якщо її розв’язок знаходити простіше.
Для розв’язування двоїстої задачі використовується двоїстий симплекс-метод, суть якого полягає в наступному.
Для запису двоїстої симплекс-таблиці потрібно, щоб задача була двоїсто-допустимою, тобто pk ³0 для всіх коефіцієнтів функції мети G (u).
Для розв’язку двоїстої задачі будемо йти тим же шляхом, що і при розв’язку задачі симплекс-методу, проте з деякими особливостями:
1) Знайдемо ведучий рядок. Його вибираємо з умови, що bi <0, причому, вибираємо рядок з найменшим bi. Номер цього рядка i* буде номером ведучого рядка.
2) Знайдемо ведучий стовпчик. Для цього розглянемо для всіх від’ємних чисел ведучого рядка (якщо таких нема, то задача не має розв’язку) частки виду  і виберемо найменшу з них. Номер стовпчика з цією часткою і буде номером ведучого стовпчика j*.
і виберемо найменшу з них. Номер стовпчика з цією часткою і буде номером ведучого стовпчика j*.
Ведучий елемент ai*j* буде від’ємним.
3) Замінюємо базис за правилами задачі симплекс-методу.
Двоїстий симплекс-метод вважається завершеним, якщо всі bi в правій частині двоїстої симплекс-таблиці стануть невід’ємними.
Розглянемо приклад розв’язку двоїстої задачі.
Приклад. Розв’язати двоїсту задачу лінійного програмування:
G (u)=3 u 1+ u 3–2 u 4®max
2 u 1+ u 2– u 4=3
–2 u 1– u 3+2 u 4+ u 5=1
u 3–2 u 4+ u 6=10
u 1³0, …, u 6³0
Побудуємо симплекс-таблицю двоїстого симплекс-методу (Рис. 2.9).
| -2 | ||||
| –1 | ||||
| –1 | –2 | –2 | ||
| –20 | ||||
| 3:|-1| | 10:|-2| |
Рис. 2.9.
Ведучою стрічкою буде стрічка з індексом 4 (оскільки b 4=–2). Ведучим стовпчиком буде стовпчик з індексом 2 (оскільки  ). Тоді ведучий елемент буде знаходитися на перетині знайдених рядка та стовпчика. Замінимо індекси ведучих рядка та стовпчика та знайдемо елементи нової таблиці (Рис. 2.10).
). Тоді ведучий елемент буде знаходитися на перетині знайдених рядка та стовпчика. Замінимо індекси ведучих рядка та стовпчика та знайдемо елементи нової таблиці (Рис. 2.10).
| -1 | ||||
| -1 | -2 | |||
| –26 |
Рис. 2.10.
Приклад. Розв’язати задачу лінійного програмування:
Q (х)=19 x 1+21 x 2®min
 2 x 1+5 x 2³20
2 x 1+5 x 2³20
4 x 1+ x 2³20
x 1 ³0, x 2³0
Запишемо задачу в канонічному вигляді:
Q (x)=19 x 1+21 x 2+0× x 3+0× x 4®min
 2 x 1+5 x 2– x 3 =20
2 x 1+5 x 2– x 3 =20
4 x 1+ x 2 – x 4=20
x 1 ³0, …, x 4³0
або
Q (x)=19 x 1+21 x 2+0× x 3+0× x 4®min
 –2 x 1–5 x 2+ x 3 =–20
–2 x 1–5 x 2+ x 3 =–20
–4 x 1– x 2 + x 4=–20
x 1 ³0, …, x 4³0
Побудуємо для неї двоїсту:
G (u)=–20 u 1–20 u 2®max
 –2 u 1–4 u 2³19
–2 u 1–4 u 2³19
–5 u 1– u 2³21
u 1³ 0, u 2³ 0
Введемо для двоїстої задачі нові базисні змінні та утворимо двоїсту симплекс-таблицю (Рис. 2.11).
| –2 | –5 | –20 | |
| –4 | –1 | –20 | |
Рис. 2.11.
Оскільки
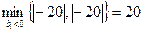 ,
,
то можна вибрати або першу, або другу стрічку в ролі ведучої. Виберемо такою першу стрічку. Так як
 ,
,
то ведучим стовпчиком буде стовпчик з індексом 2.
Після перерахунку одержимо таку таблицю (Рис. 2.12).

| 
| ||

| 
| –16 | |
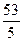
| 
| –84 |
Рис. 2.12.
Одержана таблиця не відповідає оптимальному розв’язку. Шукаємо
 .
.
Ведучою стрічкою буде стрічка з індексом 4. Для знаходження ведучого стовпчика шукаємо
 .
.
Тому ведучим стовпчиком буде з індексом 1. Після обчислень одержимо таку таблицю (Рис. 2.13).

| 
| 
| |

| 
| 
| |

| 
| 
|
Рис. 2.13.
Таким чином, оптимальний розв’язок початкової задачі буде мати вигляд  .
.
Оскільки одержано симплекс-таблицю з додатними bi, то це означає, що максимуму досягнуто. Розв’язком двоїстої задачі лінійного програмування буде точка з координатами  ,
,  , u 3=0, u 4=0, значенням функції мети у цій точці буде число G 0=
, u 3=0, u 4=0, значенням функції мети у цій точці буде число G 0=  .
.
? Контрольні запитання
- Що таке екстремум?
- Як формулюється задача математичного програмування?
- Що таке допустима область?
- Як сформулювати задачу лінійного програмування в загальному вигляді?
- Які є види розв’язків задачі лінійного програмування?
- Яка геометрична інтерпретація задачі лінійного програмування?
- Який повинен бути вигляд задачі лінійного програмування для її розв’язку симплекс-методом?
- Які основні елементи симплекс-таблиці? Як заповнити симплекс-таблицю?
- У якому випадку задача лінійного програмування буде розв’язаною?
- У якому випадку оптимальний розв’язок буде відсутнім? Як це видно з симплекс-таблиці?
- Що таке двоїста задача лінійного програмування?
- Сформулюйте теореми двоїстості.
- Чим відрізняється двоїстий симплекс-метод від звичайного?
Транспортна задача
2.2.1. Транспортна задача – частковий випадок задачі лінійного програмування
Одним із типів задач лінійного програмування є так звана лінійна транспортна задача. Класична постановка транспортної задачі полягає в наступному: потрібно перевезти товар з m складів до n споживачів. Кожен склад містить товар в кількості bi, 1£ i £ m. Кожен споживач може прийняти товар у кількості aj, 1£ j £ n. Вартість перевезення одиниці продукції з i -го складу до j -го споживача становить pij і вважається, що транспортні витрати лінійно залежать від кількості перевезеного товару. Розв’язком задачі є такий план перевезень, при якому сумарна вартість перевезень є мінімальною.
Кількість товару, перевезеного з з i -го складу до j -го споживача невідома та позначається змінною xij.
Лінійну транспортну задачу можна записати у вигляді
 , (2.11)
, (2.11)
 ,
,
xij ³0, 1£ i £ m, 1£ j £ n,
 (2.12)
(2.12)
Зауваження. Для розв’язку транспортної задачі також істотною є умова рівності кількості товару на складах та потреб споживачів, тобто
 .
.
Якщо кількість товару на складах більша необхідної кількості для споживачів, тобто
 ,
,
то товару на складі більше, ніж необхідно. Задача може бути розв’язана, якщо ввести “фіктивного” споживача, який може прийняти надлишки, при цьому вартість перевезення з будь-якого складу до цього споживача дорівнює 0.
Якщо ж
 ,
,
то це означає, що задача не має розв’язку, оскільки не всі споживачі можуть бути забезпечені товаром. Проте у деяких випадках вона також може бути розв’язана аналогічним введенням “фіктивного” складу, який містить товар, якого бракує, при цьому вартість перевезення з цього складу до будь-якого споживача дорівнює 0.
Транспорту задачу найзручніше задавати у вигляді транспортної таблиці та таблиці вартостей перевезень (Рис. 2.14). Початковими даними є числа ai, bj, pij. Для розв’язування у транспортну таблицю потрібно вписати значення xij.
| a 1 | a 2 | … | an | |
| b 1 | x 11 | x 12 | x 1 n | |
| … | ||||
| bm | xm 1 | xm 2 | xmn |
| p 11 | p 12 | … | p 1 n |
| … | … | ||
| pm 1 | pm 2 | pmn |
Рис. 2.14. Транспортна таблиця та таблиця вартості перевезень.
Ці таблиці можна об’єднати в одну (Рис. 2.15).
| a 1 | a 2 | … | … | … | an | |||||||
| p 11 | p 12 | p 1 n | ||||||||||
| b 1 | x 11 | x 12 | x 1 n | |||||||||
| … | ||||||||||||
| pm 1 | pm 2 | pmn | ||||||||||
| bm | xm 1 | xm 2 | xmn |
Рис. 2.15. Об’єднана транспортна таблиця.
Приклад. Нехай транспортна задача задана у вигляді двох таблиць (Рис. 2.16).
Рис. 2.16.
У об’єднаній транспортній таблиці (Рис. 2.17) задача матиме вигляд
Рис. 2.17.
Надалі будемо використовувати об’єднану транспортну таблицю.
Таким чином, транспортна задача є задачею лінійного програмування, розв’язування якої полягає у знаходженні таких значень
змінних (при накладених на них обмеженнях), при яких функція мети K досягає мінімуму.
Дата публикования: 2015-10-09; Прочитано: 2359 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
