Обратная функция

Обратная функция x = φ (y)

Пусть даны два множества Х и Y. Обратной по отношению к y = f (x) называется функция x = φ (y), которая каждому ставит в соответствие такое 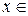Х, что f (x) = y; обозначается y = (f (x))-1 или y = f -1(x) (т.е. будем считать у – независимой переменной, а х – зависимой, тогда х является функцией переменной у, обратной к данной).

Таким образом, для нахождения функции x = φ (y), обратной к функции y = f (x), нужно решить уравнение f (x) = y относительно х. При этом следует помнить, что для функции y = f (x) обратная функция x = φ (y) может быть многозначной.

Примеры: 1) Функция является обратной к y = 2 x + 3.

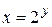2) Функция является обратной к . 3) Функция является обратной к . 4) Для функции обратной является многозначная функция при .

Графики взаимообратных функций y = f (x) и x = φ (y) симметричны относительно прямой y = x.