Теорема 3

Якщо вектори 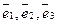некомпланарні, то для будь-якого вектора 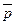існують єдині числа 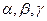такі, що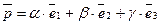

Координати вектора.

Нехай вектори 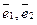утворюють базис площини. Тоді згідно теореми 2 будь-який вектор 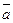площини утворюється як лінійна комбінація базисних векторів: 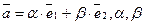- єдині (1).

Числа 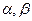називаються координатами вектора 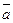в базисі 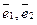. Позначають: =(.

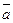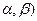Очевидно, що нуль-вектор має нульові координати. Базисні вектори мають координати: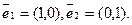

Аналогічно, згідно теореми 3, для будь-якого вектора 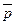у просторі існують єдині числа 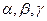, такі, що 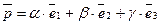(2).

Числа 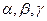називаються координатами вектора 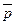в базисі 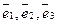. Позначають: =().

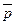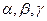Базисні вектори у просторі мають координати: 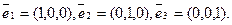Рівні вектори мають однакові відповідні координати.

Вирази (1),(2) називаються розкладом вектора по базису.