 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Замена переменных в неопределенном интеграле
|
|
Один из приемов, часто используемых при вычислении интегралов− замена переменной. Он основывается на следующей теореме.
Теорема 1. Пусть  − первообразная для
− первообразная для 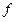 . Если
. Если  − дифференцируемая функция, то
− дифференцируемая функция, то
 .
.
В частности,
 (1)
(1)
Пример 1. Найти 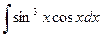 .
.
Решение. Положим 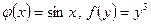 . Тогда
. Тогда  . Так как
. Так как 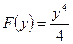 , то по Теореме 1
, то по Теореме 1  .
.
Обычно эти выкладки записываются по следующей схеме: положим  ; тогда
; тогда 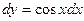 и тем самым
и тем самым
 .
.
В процессе решения мы 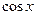 внесли под знак дифференциала, поэтому и метод нахождения неопределенного интеграла, основанный на Теореме 1, называется “ внесением под знак дифференциала”.
внесли под знак дифференциала, поэтому и метод нахождения неопределенного интеграла, основанный на Теореме 1, называется “ внесением под знак дифференциала”.
Пример 2. Найти 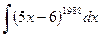 .
.
Решение. Полагая  ,
, 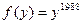 и применяя формулу (1), получаем
и применяя формулу (1), получаем

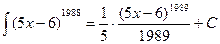 .
.
Пример 3. Найти 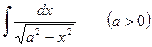 .
.
Решение.  .
.
Пример 4. Найти 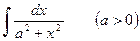 .
.
Решение. 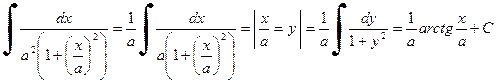 .
.
Пример 5. 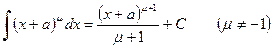 ,
,
 .
.
Решение. Применим формулу (1) и табличные интегралы 1 и 2, учитывая, что коэффициент перед 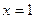 .
.
Пример 6. Найти 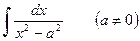 .
.
Решение. 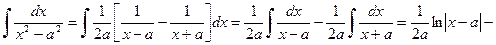
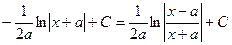 .
.
Иногда правило замены переменной удобно использовать в другой форме.
Теорема 2. Пусть функция 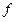 имеет примитивную на
имеет примитивную на 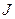 ,
, 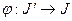 –строго монотонная функция, дифференцируемая на
–строго монотонная функция, дифференцируемая на 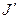 ,
, 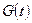 –примитивная функции
–примитивная функции 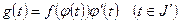 . Тогда
. Тогда  есть примитивная функции
есть примитивная функции 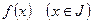 , т. е.
, т. е.  .
.
Доказательство. Обозначим через  первообразную функции
первообразную функции 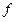 .Тогда по Теореме 1
.Тогда по Теореме 1  , откуда
, откуда 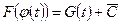 для
для 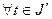 . Рассмотрим
. Рассмотрим  . Тогда
. Тогда 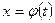 для некоторого
для некоторого  , а это
, а это  . Поэтому
. Поэтому  , и тем самым
, и тем самым  есть первообразная функции
есть первообразная функции 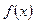 .
.
При применении этой теоремы выкладки записываются по следующей схеме. Требуется вычислить 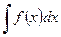 . Положим
. Положим 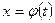 . Тогда
. Тогда  . В результате формальной подстановки находим
. В результате формальной подстановки находим 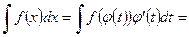
 . Подставляя
. Подставляя  , получаем окончательный результат.
, получаем окончательный результат.
Пример 1. Вычислить  .
.
Решение. Используем подстановку  (считая
(считая 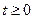 ), которая позволяет избавиться под знаком интеграла от корня. Тогда
), которая позволяет избавиться под знаком интеграла от корня. Тогда 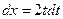 и
и
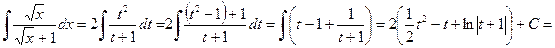
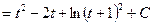 .
.
Чтобы получить выражение найденного интеграла через 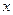 , следует подставить
, следует подставить 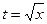 . Таким образом
. Таким образом
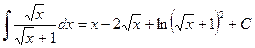 .
.
Пример 2. Вычислить интеграл 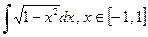 .
.
Решение. Пусть 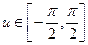 . Имеем
. Имеем
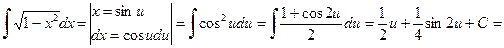
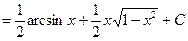 .
.
Дата публикования: 2015-09-18; Прочитано: 255 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
