 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Спеціальні бінарні відношення
|
|
Нехай 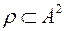 ,
, 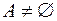 .
.
Означення. Відношенням еквівалентності називається бінарне відношення 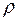 на множині
на множині 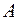 , якщо воно рефлексивне, симетричне і транзитивне, тобто:
, якщо воно рефлексивне, симетричне і транзитивне, тобто:
1) 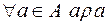 ;
;
2) 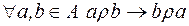 ;
;
3)  .
.
Відношення еквівалентності є узагальненням відношення = на між числами або множинами.
Приклади:
1. Відношення рівності на будь-якій числовій множині.
2. Відношення ‘‘мати ту саму остачу від ділення на 7’’ на множині 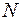 .
.
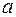 множини
множини 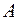 називається множина всіх елементів множини
називається множина всіх елементів множини 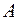 , які еквівалентні
, які еквівалентні 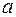 . Позначається
. Позначається 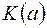 .
. 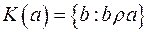 . Означення. Розбиттям непорожньої множини
. Означення. Розбиттям непорожньої множини 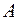 називається сукупність таких її непорожніх підмножин
називається сукупність таких її непорожніх підмножин  , які не перерізаються (
, які не перерізаються ( 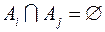 ), а в об’єднанні складають всю множину
), а в об’єднанні складають всю множину 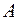 (
(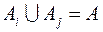 ). Приклад.
). Приклад. 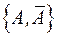 – розбиття універсуму. Теорема. Сукупність всіх класів еквівалентності є розбиттям множини
– розбиття універсуму. Теорема. Сукупність всіх класів еквівалентності є розбиттям множини 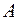 . Справедливе і обернене: Нехай
. Справедливе і обернене: Нехай 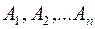 – довільне розбиття множини
– довільне розбиття множини 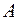 і для будь-яких елементів
і для будь-яких елементів 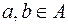 задане бінарне відношення
задане бінарне відношення 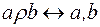 належать одному й тому ж класу розбиття. Тоді
належать одному й тому ж класу розбиття. Тоді 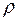 є відношенням еквівалентності. Означення. Множина всіх класів еквівалентності деякої множини
є відношенням еквівалентності. Означення. Множина всіх класів еквівалентності деякої множини 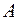 , утворених за відношенням еквівалентності
, утворених за відношенням еквівалентності 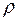 , називається фактормножиною множини
, називається фактормножиною множини 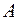 за даним відношенням еквівалентності. Позначається
за даним відношенням еквівалентності. Позначається 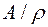 . З поняття рівності між числами випливає більш широке поняття відношення еквівалентності на множинах. За аналогією нерівності також можуть бути використані як моделі для більш широкого класу відношень – відношень порядку на множинах.
. З поняття рівності між числами випливає більш широке поняття відношення еквівалентності на множинах. За аналогією нерівності також можуть бути використані як моделі для більш широкого класу відношень – відношень порядку на множинах. Означення. Відношенням нестрогого порядку називається бінарне відношення 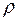 на множині
на множині 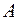 , якщо воно рефлексивне, антисиметричне і транзитивне, тобто:
, якщо воно рефлексивне, антисиметричне і транзитивне, тобто:
1) 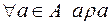
2) 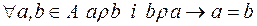 ;
;
3) 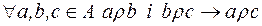 .
.
Означення. Відношенням строгого порядку називається бінарне відношення 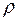 на множині
на множині 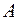 , якщо воно антирефлексивне, асиметричне і транзитивне, тобто
, якщо воно антирефлексивне, асиметричне і транзитивне, тобто
1) 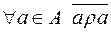
2) 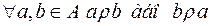 ;
;
3) 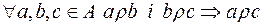 .
.
Означення. Множина 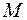 , на якій задане відношення порядку, називається цілком впорядкованою, якщо будь-які два елементи з
, на якій задане відношення порядку, називається цілком впорядкованою, якщо будь-які два елементи з 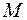 знаходяться в цьому відношенні і частково впорядкованою в противному випадку.
знаходяться в цьому відношенні і частково впорядкованою в противному випадку.
Приклад:  і
і  – відношення нестрогого порядку для чисел;
– відношення нестрогого порядку для чисел;  і
і 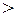 – відношення строгого порядку. Обидва відношення цілком впорядковують множини
– відношення строгого порядку. Обидва відношення цілком впорядковують множини 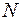 і
і 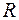 .
.
Дата публикования: 2015-09-18; Прочитано: 775 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
