Властивості бінарних відношень. Нехай – бінарне відношення на довільній множині ( )

Нехай 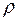– бінарне відношення на довільній множині ().

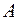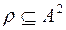Означення. Відношення 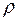називається рефлексивним, якщо воно завжди виконується між елементом і ним самим. ().

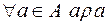Приклад. Відношення нестрогої нерівності на множинах .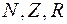

Означення. Відношення 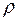називається антирефлексивным, якщо воно не виконується для будь-якого елемента. ().

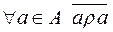Приклад. Відношення строгої рівності на множинах .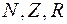

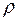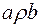Означення. Відношення називається симетричним, якщо для будь-яких елементів при виконанні виконується . ().

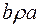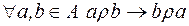Приклад. Відношення рівності на множинах .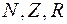

Означення. Відношення 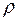називається антисиметричним, якщо 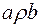і 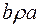виконуються одночасно тоді і тільки тоді, коли . ()

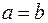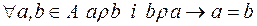Приклад: Відношення нестрогої нерівності на числових множинах :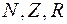

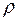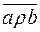Означення. Відношення називається асиметричним, якщо для будь-яких елементів або або . ()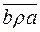

Приклад. Відношення строгої нерівності на числових множинах :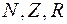

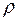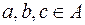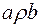Означення. Відношення називається транзитивним, якщо для будь-яких з і 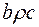випливає . ()

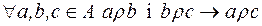Приклад. Відношення =, .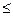

Наявність певної властивості легко прослідкувати за матрицею або за графом відношення.