| 1. Рівняння, їх розв'язування
|
| Означення
| Приклади
|
| Рівняння – це рівність, яка містить змінну.
Розв’язок рівняння – це значення змінної, при якому рівняння перетворюється у правильну рівність.
| 3(х – 4) = 24,
(х – 4) = 24: 3,
х – 4 = 8,
х = 8 + 4,
х =12 – розв’язок рівняння
|
| Розв’язати рівняння – це означає знайти його розв’язки або довести, що їх немає.
| 3(х – 4) = 24, х =12
|
| Рівносильні рівняння – це рівняння, які мають одні і ті самі розв’язки.
| 3х = 36 і 3(х – 4) = 24;
їх розв’язок х =12
|
| Деякі властивості рівнянь
|
| У будь-якій частині рівняння можна звести подібні доданки. Якщо з однієї частини рівняння перенести доданки в іншу частину і при цьому змінити знаки доданків на протилежні, отримаємо рівняння, рівносильне даному.
| 3х – 4 +5х = 36
3х + 5х = 36 + 4
8х = 40
|
| При діленні (множенні) обох частин рівняння на одне і те саме число, відмінне від нуля, отримаємо рівняння, рівносильне даному.
| Поділимо обидві частини рівняння 8х = 40 на 8:
х = 5 – це рівняння рівносильне 8х = 40, їх розв’язок 5.
|
| 2. Нерівності, їх розв'язування
|
| Якщо а менше b або а більше b, то записують так: а < b або а > b. Такий вираз називається нерівністю.
| 7 < 10; 8 > 7
|
| Знаки <, > називаються знаками строгих нерівностей.
| а < b; а > b
|
Знаки  , ,  називаються знаками нестрогих нерівностей. називаються знаками нестрогих нерівностей.
| а  b; а b; а  b b
|
| 3. Лінійні рівняння
|
| Рівняння виду ax = b, де х - змінна, а і b - деякі числа, називається лінійним рівнянням.
| 4- 5х = 6 – 2(х + 2),
-3х = -2
х = 
|
| Розв’язування лінійних рівнянь
|
| ax + b = 0;
ax = - b
| 5х + 4 = 0,
5х = -4
|
a 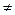 0; х = - 0; х = -  - єдиний розв’язок - єдиний розв’язок
| х = -  - розв’язок - розв’язок
|
| а = 0, 0х = - b – немає розв’язків
| 0х = -10
немає розв’язків – 10 на 0 поділити неможливо
|
а = 0, b = 0. 0  х = 0 – нескінчена множина розв’язків х = 0 – нескінчена множина розв’язків
| 7х = 7х,
7х - 7х = 0,
0х = 0 х – будь-яке число
|
| Розв’язування лінійних рівнянь з двома змінними
|
| Лінійним рівнянням з двома змінними х и у називається рівняння виду: ах + bу + с = 0, де х и у - змінні, а, b, с – деякі числа.
| 3х + 4у + 5 = 0 – лінійне рівняння
|
| Розв’язком рівняння з двома змінними називається будь-яка пара чисел (х; у), яка перетворює рівняння на тотожність.
Розв’язати рівняння з двома змінними – означає знайти всі пари чисел (х; у), які є його розв’язком.
| х + 2у = 5 – лінійне рівняння
Пара (1; 2) – розв’язок рівняння
|
| 4. Лінійні нерівності
|
Лінійною називається нерівність виду ах > b
( або, відповідно, ах < b, ах  b, ах b, ах  b), де b), де  - числа. - числа.
|
| Розв’язками нерівності з однією змінною називається множина таких значень змінної, яка перетворює її на правильну числову нерівність.
|
| Властивості
| Приклади
|
| Якщо з однієї частини нерівності перенести в іншу доданок з протилежним знаком, то утвориться нерівність, рівносильна даній
| 4(у - 1) + 7  1 – 3(у + 2),
4у – 4 + 7 1 – 3(у + 2),
4у – 4 + 7  1 – 3у – 6,
4у + 3у 1 – 3у – 6,
4у + 3у  1 – 6 – 7. 1 – 6 – 7.
|
| Якщо обидві частини нерівності помножити або поділити на одне й те саме додатне число, то утвориться нерівність, рівносильна даній
| 7у  -8,
у -8,
у  - - 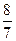

|
| Якщо обидві частини нерівності помножити або поділити на одне й те саме від’ємне число, змінивши при цьому знак нерівності на протилежний, то отримуємо рівносильну даній нерівність.
| - 3х + 8 < 2х – 2,
- 5х < -10,
х > 2

|
| 5. Квадратні рівняння
|
Рівняння виду ах2 + bх + с = 0, де х - змінна, а, b, с – деякі числа, причому а 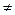 0, називають квадратним рівнянням.
а – перший коефіцієнт, b – другий коефіцієнт, с – вільний член 0, називають квадратним рівнянням.
а – перший коефіцієнт, b – другий коефіцієнт, с – вільний член
|
|
| Якщо в цьому рівнянні хоча б один з коефіцієнтів дорівнює нулю, то дане рівняння називають неповним квадратним рівнянням. Неповні квадратні рівняння бувають трьох видів:
1) ах2 = 0; 2) ах2 + bх = 0; 3) ах2 + с = 0
|
| ах2 = 0 при b = 0, с = 0
х2 = 0
х = 0
рівняння має тільки один розв’язок
| 5х2 = 0
х2 = 0
х = 0
|
ах2 + bх = 0 при с = 0
х(ах + b) = 0
х1 = 0 або х2 =  рівняння завжди має два розв’язки
рівняння завжди має два розв’язки
| 4х2 + 3х = 0
х(4х + 3) = 0
х1 = 0 або х2 = 
|
ах2 + с = 0 при b = 0
ах2 = - с
х2 = -  оскільки с
оскільки с 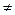 0, то - 0, то -  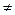 0, тоді:
1) якщо - 0, тоді:
1) якщо -  > 0, то рівняння має два розв’язки
х1 = - > 0, то рівняння має два розв’язки
х1 = -  ; х2 = ; х2 =  ;
2) якщо - ;
2) якщо -  < 0, то рівняння не має розв’язків < 0, то рівняння не має розв’язків
| 9х2 - 4 = 0
9х2 = 4
х2 =  х1 = -
х1 = -  ; х2 = ; х2 =  ;
16х2 + 9 = 0
16х2 = - 9
х2 = - ;
16х2 + 9 = 0
16х2 = - 9
х2 = -  немає розв’язків
немає розв’язків
|
| Якщо а =1, то квадратне рівняння називають зведеним
| х2 -bх + 30 = 0
|
Повні квадратні рівняння ах2 + bх + с = 0 розв’язуємо за формулою х1,2 =  ,
де D = ,
де D =  називають дискримінантом даного квадратного рівняння називають дискримінантом даного квадратного рівняння
|
| Якщо D < 0, то рівняння не має дійсних розв’язків
| 2х2 + 5х + 6 = 0
D = 25 – 48 = - 23
D < 0, отже, рівняння не має дійсних розв’язків
|
Якщо D = 0, то рівняння має два однакові розв’язки:
х1 = х2 = 
| 4х2 + 4х + 1 = 0
D = 16 – 16 = 0
D = 0, отже, рівняння має два однакові розв’язки:
х1 = х2 = 
|
Якщо D > 0, то рівняння має два різні розв’язки:
х1 =  , х2 = , х2 =  , ,
| 2х2 + 3х + 1 = 0
D = 9 – 8 = 1, D > 0, отже, рівняння має два різні розв’язки:
х1 = 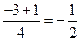 , х2 = , х2 = 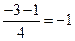 . .
|
| Теорема Вієта
|
ах2 + bх + с = 0, 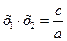 , ,  Якщо а = 1, то
Якщо а = 1, то  , , 
|
|
| 6. Рівняння, що зводяться до квадратних
|
Рівняння виду ах4 + bх2 + с = 0, де а 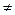 0, b 0, b 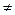 0 називається біквадратним рівнянням 0 називається біквадратним рівнянням
| 2х4 + 3х2 + 4 = 0
|
Формула розкладу квадратного тричлена на множники: ах2 + bх + с =а( )( )( ) )
| 2х2 - х - 3 =2( )( )( );
2х2 - х - 3 =0,
х1 = 1,5; х2 = - 1
2х2 - х - 3 =2( );
2х2 - х - 3 =0,
х1 = 1,5; х2 = - 1
2х2 - х - 3 =2( )( )( ). ).
|
| 7. Квадратні нерівності
|
Нерівність виду ах2 + bх + с < 0(ах2 + bх + с>0), де х - змінна, а, b, с – деякі числа, причому а 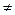 0, називають квадратною. 0, називають квадратною.
| 3х2 + 4х - 5 < 0
- 5х2 - 6х+7 > 0
|
| Для розв’язування квадратичних нерівностей використовують ескіз графіка функції
у = ах2 + bх + с, тобто параболу
|  х
х  
| 3х2 - 7х - 10  0
у = 3х2 - 7х – 10 – графік - парабола, вітки напрямлені вгору, вісь Ох перетинає в точках 0
у = 3х2 - 7х – 10 – графік - парабола, вітки напрямлені вгору, вісь Ох перетинає в точках
|

 ,
,  називаються знаками нестрогих нерівностей.
називаються знаками нестрогих нерівностей.
 b; а
b; а  b
b

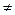 0; х = -
0; х = -  - єдиний розв’язок
- єдиний розв’язок
 - розв’язок
- розв’язок
 х = 0 – нескінчена множина розв’язків
х = 0 – нескінчена множина розв’язків
 b, ах
b, ах  b), де
b), де  - числа.
- числа.
 1 – 3(у + 2),
4у – 4 + 7
1 – 3(у + 2),
4у – 4 + 7  1 – 3у – 6,
4у + 3у
1 – 3у – 6,
4у + 3у  1 – 6 – 7.
1 – 6 – 7.
 -8,
у
-8,
у  -
- 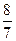


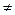 0, називають квадратним рівнянням.
а – перший коефіцієнт, b – другий коефіцієнт, с – вільний член
0, називають квадратним рівнянням.
а – перший коефіцієнт, b – другий коефіцієнт, с – вільний член
 рівняння завжди має два розв’язки
рівняння завжди має два розв’язки

 оскільки с
оскільки с 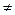 0, то -
0, то - 
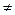 0, тоді:
1) якщо -
0, тоді:
1) якщо -  > 0, то рівняння має два розв’язки
х1 = -
> 0, то рівняння має два розв’язки
х1 = -  ; х2 =
; х2 =  ;
2) якщо -
;
2) якщо -  < 0, то рівняння не має розв’язків
< 0, то рівняння не має розв’язків
 х1 = -
х1 = -  ; х2 =
; х2 =  ;
16х2 + 9 = 0
16х2 = - 9
х2 = -
;
16х2 + 9 = 0
16х2 = - 9
х2 = -  немає розв’язків
немає розв’язків
 ,
де D =
,
де D =  називають дискримінантом даного квадратного рівняння
називають дискримінантом даного квадратного рівняння


 , х2 =
, х2 =  ,
,
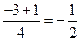 , х2 =
, х2 = 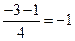 .
.
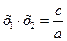 ,
,  Якщо а = 1, то
Якщо а = 1, то  ,
, 
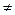 0, b
0, b 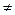 0 називається біквадратним рівнянням
0 називається біквадратним рівнянням
 )(
)( )
)
 )(
)( );
2х2 - х - 3 =0,
х1 = 1,5; х2 = - 1
2х2 - х - 3 =2(
);
2х2 - х - 3 =0,
х1 = 1,5; х2 = - 1
2х2 - х - 3 =2( )(
)( ).
).
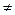 0, називають квадратною.
0, називають квадратною.
 х
х 

 0
у = 3х2 - 7х – 10 – графік - парабола, вітки напрямлені вгору, вісь Ох перетинає в точках
0
у = 3х2 - 7х – 10 – графік - парабола, вітки напрямлені вгору, вісь Ох перетинає в точках
