Метод нелинейного преобразования, обратного функции распределения

Задачи моделирования случайных процессов, имеющих место в системах передачи и обработки сигналов, часто приводят к необходимости получения СВ с негауссовским законом распределения. Наиболее эффективным аналитическим методом получения негауссовских СВ является метод монотонного нелинейного преобразования (метод обратных функций).

Найдем закон распределения величины y полученной нелинейным преобразованием непрерывной СВ x (рис. 2.1). Будем считать, что существует взаимно однозначное преобразование . Обратное преобразование обозначим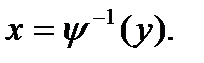

Рис. 1. Функциональное преобразование случайной величины

Из рис. 1 видно, что всегда, когда СВ x попадает в интервал СВ y попадает в интервал . Поэтому выполняется равенство , откуда следует, что и при получаем соотношение

(1)

Рассмотрим типичный пример получения СВ с заданным законом распределения из СВ с равномерным распределением. Пусть задана СВ x с равномерным законом распределения w (x)=1, x ∈[0, 1], необходимо получить случайное число y с заданным законом распределения w (y), которому соответствует некоторое нелинейное преобразование, например, . Далее по формуле (1) получаем плотность вероятности

Теперь решим обратную задачу: найдем вид преобразования ψ(x) по заданной плотности распределения , y = ψ(x). Для этого проинтегрируем левую и правую части (1)

(2)

откуда находим функцию распределения F (y), тогда СВ y можно найти с помощью преобразования y = ψ(x).

Описанный выше метод моделирования называется методом обратных функций. Для моделирования СВ с заданной функцией распределениянеобходимо осуществить нелинейное преобразование вида

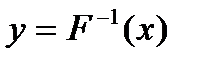
(3)

Формула (3) означает решение уравнения

(4)

где означает, что СВ x имеет равномерное распределение на отрезке [0, 1].

Комбинируя формулы (2) и (3), можно по реализации СВ x с произвольной функцией распределения моделировать величины с требуемой функцией распределения F (y). Моделирующий алгоритм дает суперпозиция нелинейных преобразований (2) и (3):

Получим с помощью метода обратных функций моделирующие алгоритмы для ряда распределений, используемых при моделировании случайных процессов и полей.

Рассмотрим СВ с рэлеевским законом распределения. В этом случае плотность распределения вероятностей (ПРВ), функция распределения, среднее значение и дисперсия имеют соответственно вид:

,

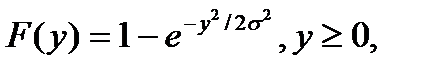
где σ — параметр рэлеевского распределения. При этом СВ y можно получить решая уравнение (4), откуда получаем:

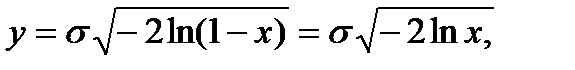
(5)

где x - равномерно распределенная в интервале [0, 1] СВ (переход от ln(1− x) к ln x в последней формуле основан на том, что СВ 1− x и x имеют здесь одинаковые законы распределения).

Аналогично, для получения СВ, описывающей интервалы времени между соседними заявками, поступающими на вход телекоммуникационной системы и имеющей показательный закон распределения

, y ≥ 0,

решая уравнение F (y) = x, т.е. , находим обратную функцию Таким образом, показательную СВ y можно сформировать из равномерной СВ x с помощью функционального преобразования

Путём преобразований

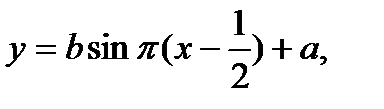
(6)

можно сформировать СВ, распределенные соответственно по закону арксинуса

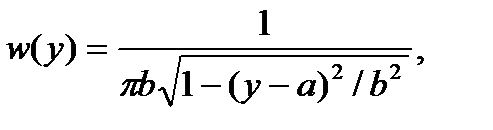
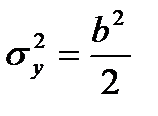
и закону Коши

Используя свойство симметрии тригонометрических функций, нетрудно убедиться, что закон распределения СВ у, формируемых согласно алгоритмам (6), не изменится, если аргумент π(x −1/ 2) у тригонометрических функций заменить аргументом 2 π x.

Рассмотрим СВ y, имеющую ПРВ:

Соответствующая функция распределения

Уравнение (2) в данном случае примет вид

Находя отсюда y, получим

где , r > 0.

Рассмотрим моделирование СВ с плотностью

(7)

Интегрируя формулу (2.7), получим для функции распределения выражение

Отсюда получаем уравнение

из которого следует моделирующий алгоритм

К сожалению, не всегда существуют элементарные преобразования для получения СВ с заданным законом распределения из равномерно распределенных СВ. В частности, у СВ с нормальным распределением функция, обратная функции распределения, не выражается через элементарные функции. В подобных случаях для формирования СВ с заданным распределением используются различные аппроксимации функции , а также другие подходы к решению задачи моделирования.