Метод кусочной аппроксимации

Существуют различные приближенные приемы моделирования СВ:численноерешение уравнения x = F (y) относительно y при использованииметода нелинейного преобразования, обратного функции распределения;замена непрерывных распределений соответствующими дискретнымираспределениями, для которых можно указать достаточно простыемоделирующие алгоритмы и другие приёмы. Среди них универсальным инаиболее простым является метод кусочной аппроксимации.

Сущность этого метода состоит в следующем. Пусть требуется получитьСВ y с функцией плотности w (y). Предположим, что область возможныхзначений СВ y ограничена интервалом (a, b) (неограниченное распределениеможно приближенно заменить ограниченным). Разобьем интервал (a, b) на n достаточно малых интервалов (am, am +1),

m =0,..., n −1, a 0 = a, an = b, так, чтобы распределение заданной СВ в пределах этих интервалов можно былодовольно точно аппроксимировать каким-нибудь простым распределением(рис. 3), например, равномерным, трапецеидальным и т. д. В дальнейшем

рассмотрим кусочную аппроксимацию равномерным распределением.

Пусть Pm - вероятность попадания СВ y в каждый из интервалов (am, am +1). Получатьреализации величины y с кусочно-равномерным распределением можно, очевидно, в соответствии со следующей схемой преобразования случайных чисел: 1) случайным образом с вероятностью Pm выбирается интервал (am, am +1); 2) формируется реализация СВ,равномерно распределенной в интервале ; 3) искомаяреализация получается по формуле

Случайный выбор интервала (am, am +1) с вероятностью Pm означает, по существу, моделирование дискретной СВ, принимающей n значений am, m = 0,..., n −1, x 0 =0, xn =, с вероятностью Pm каждое, что можно сделать достаточно просто. Интервал (0, 1) разбивается на n интервалов (xm, xm +1), m = 0,..., n −1, x 0 =0, xn =1, длиной (xm +1− xm)= Pm каждый. Из датчика случайных, равномерно распределенных в интервале (0, 1) чисел выбирается некоторая реализация . Путем последовательного сравнения с xm определяется тот интервал (xm, xm +1), в котором находится .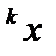

B основу этого процесса положен очевидный факт: вероятность попаданияравномерно распределенной в интервале (0, 1) СВ в некоторый подынтервал(xm, xm +1)равна длине этого подынтервала. Рассмотренный выше процесспредставляет интерес не только как составной элемент метода кусочнойаппроксимации, он широко используется в качестве алгоритма длямоделирования дискретных СВ и случайных событий.

Для моделирования СВ методом кусочной аппроксимации наиболее удобно при машиннойреализации выбирать вероятности попадания во все интервалы (am, am +1)одинаковыми Pm =1/ n,ачисло n таким,что n =2 N,где N - целое число, меньше или равное количествудвоичных разрядов чисел,вырабатываемых датчиком случайных чисел. В этом случае величины am должны быть выбраны таким образом, чтобы выполнялось равенство

При равенстве вероятностей Pm для случайного выбора индекса m можноиспользовать первые N разрядов числа, извлекаемого из датчика равномернораспределенных случайных чисел.

Используя рассмотренный прием, приходим к следующему способупреобразования равномерно распределенных случайных чисел в случайныечисла с заданным законом распределения. Из датчика равномернораспределенных в интервале (0, 1) случайных чисел извлекается парареализаций 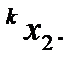Первые разрядов числа используются длянахождения адресов ячеек, в которых хранятся величины am, am +1, a затем поформуле получается реализация СВ y с заданнымзаконом распределения. Такой алгоритм является довольно экономичным поколичеству требуемых операций, которое не зависит от числа n, т. е. не зависитот точностикусочной аппроксимации. Однако с увеличением точностиаппроксимации возрастает количество ячеек памяти, требуемое для хранениявеличин am, m = 0,…, n, что является недостатком рассмотренного метода прибольших значениях n.