Устойчивость автоматических систем регулирования химико-технологических объектов

Устойчивость системы определяется характером ее свободного движения, которое описывается однородным дифференциальным уравнением динамики. Для системы n-ого порядка оно имеет вид:

где у — выходная величина; а₁, а₂,…, а_п — постоянные коэффициенты; t — время.

Исследование системы на устойчивость требует решения этого уравнения, которое может быть представлено в следующем виде:

где А_к — постоянные интегрирования, определяемые из начальных условий; р_к — корни характеристического уравнения вида:

Однако достаточно просто решаются дифференциальные уравнения только 1-го и 2-го порядков. Решение уравнений более высокого порядка требует преодоления определенных трудностей, возрастающих c повышением порядка уравнения. Значительно проще можно найти корни характеристических уравнений. Поэтому целесообразно выяснить зависимость между устойчивостью системы и значением корней ее характеристического уравнения.

Устойчивость системы и корни характеристического уравнения. Расположение корней характеристического уравнения позволяет судить об устойчивости системы. Если характеристическое уравнение имеет только вещественные и разные корни, то характер изменения каждой составляющей

зависит от знака корня характеристического уравнения р_к.

Окончательно условие устойчивости систем может быть сформулировано следующим образом. Для устойчивости системы, описываемой линейным дифференциальным уравнением с постоянными коэффициентами, необходимо и достаточно, чтобы все вещественные корни ее характеристического уравнения были отрицательными, а комплексные корни имели отрицательную вещественную часть. Если хотя бы один из вещественных корней характеристического уравнения системы положителен или одна пара сопряженных комплексных корней имеет положительную вещественную часть, то система неустойчива. Таким образом, исследование устойчивости линейной системы сводится к определению знаков вещественных частей корней характеристического уравнения.

Критерии устойчивости. С математической точки зрения критерии устойчивости представляют собой необходимые и достаточные условия, при соблюдении которых все корни характеристического уравнения системы имеют отрицательную вещественную часть.

Алгебраический критерий устойчивости, предложенный в 1895 году швейцарским математиком Гурвицем, формулирует условие устойчивости в виде определителей.

Для нахождения условий устойчивости системы n-го порядка по коэффициентам характеристического уравнения (IV,53) сначала составляют матрицу, действуя в следующем порядке. По главной диагонали матрицы (слева вниз направо) последовательно выписывают коэффициенты характеристического уравнения, начиная с а₁. Столбцы матрицы, начиная с главной диагонали, заполняют коэффициентами характеристического уравнения вверх по возрастанию индексов до а_п, а вниз — по их убыванию до а₀. Оставшиеся пустыми места заполняют нулями. Если система имеет n - ый порядок, то всего должно быть заполнено п строк и п столбцов матрицы, приведенной ниже. Затем из матрицы выделяют диагональные определители или определители Гурвица; для этого в ней отчеркивают одинаковое число строк и столбцов, начиная от левого верхнего угла матрицы. Определители Гурвица имеют вид:

Естественно, что определитель п-го порядка Δ_п включает в себя всю матрицу.

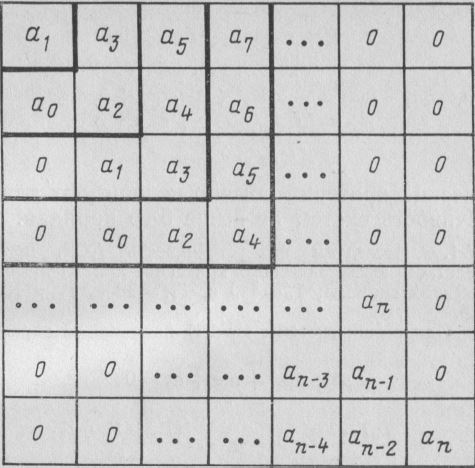
По алгебраическому критерию линейная система п-го порядка устойчива, если коэффициент а₀ и все п диагональных определителей Гурвица положительны.

Положительность определителя n-го порядка обычно не выявляют, так как он может быть представлен произведением

и, следовательно, требование его положительности сводится к требованию одновременной положительности свободного члена характеристического уровня а_п и предпоследнего определителя Δ_n-1.

Ниже приведены условия устойчивости для систем 3-го, 4-го и 5-го порядков:

для n = 3

для n = 4

для n = 5