Рекурсивные методы оптимальной оценки случайных величин

Для рекурсивной оценки параметров таких случайных объектов, как случайные величины, разработаны процедуры стохастической аппроксимации: Роббинса-Монро, Кифера-Вольфовица, Ньютона-Рафсона, Качмажа и др. Данные процедуры разработаны для нахождения корней уравнения регрессии и носят обобщенное название градиентных процедур, поскольку в процессе итерационных вычислений находится минимум функционала качества

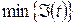: . (5.10)

Для рекурсивной оценки случайных величин используют условное среднее , где учтено, что среднее находится с учетом наблюдений :

, (5.11)

В этом случае используется критерий минимума среднеквадратического отклонения

, (5.12)

где - оценка случайных величин .

Рекурсивная процедура Роббинса-Монро на шаге представляется в виде

, (5.13)

где - уравнение наблюдения, формирующее наблюдаемую статистику, 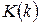- коэффициент, обеспечивающий сходимость процедуры (5.13).

На рис.5.25 представлена структурная схема процедуры (5.13).

К коэффициенту сходимости процедуры (5.13) предъявляются особые требования, обеспечивающие выполнение условий устойчивости. Этот коэффициент должен отвечать условиям Дворецкого:

. (5.14)

Если величина является аналоговой, то соответствующее (5.13) уравнение оценки примет вид:

, (5.15)

где удовлетворяет условиям:

, (5.16)

которые являются обобщением условий Дворецкого (5.14) на непрерывный случай.

Аналоговая реализация алгоритма Робинса-Монро представлена на рис.5.26.

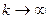Можно показать, что при условиях (5.14), (5.16) оценки (5.13) и (5.15) сходятся асимптотически, и выражение (5.12) асимптотически стремится к нулю, то есть . Иными словами, при апостериорная дисперсия , показывающая степень разброса ошибки 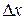, стремится к нулю. При этом крутизна данной характеристики зависит от выбора или для дискретной величины . Очевидно, коэффициент, обеспечивающий сходимость (5.14) должен быть меньше единицы, например, он может быть вида

.

Следует заметить, что все процедуры градиентного типа отличаются выбором характера зависимостей или . Так, в известной процедуре Уидроу-Хоффа .

При использовании критерия минимума среднего квадрата отклонения (5.12) рекурсивная процедура Ньютона-Рафсона на шаге представляется в виде:

, (5.17)

где определяется таким образом, чтобы второе слагаемое в правой части оказалось с отрицательным знаком,

- градиент функции . (5.18)

Рекурсивные процедуры оценки (5.13), (5.15), (5.17) и другие, так же как и оценки, полученные методами обработки выборки, имеют одинаковую эффективность и в асимптотике дают одно и то же значение .

На рис.5.27 приведен пример реализации случайной величины а), наблюдаемой величины на фоне шума б) и ее оценки согласно рекурсивной процедуре Роббинса-Монро в).

Достоинством рассмотренных рекурсивных методов оценивания, является то, что на практике они оказываются более эффективными, поскольку дают оценку в реальном масштабе времени, а не требуют потерь времени на накопление и обработку статистики. Таким образом, процедуру рекурсивной оценки можно прервать на любом этапе ее получения. Кроме того, эти рекурсивные процедуры оценки случайных величин согласуются с процедурами оценки случайных процессов. Иными словами, если есть процедура оценки случайных процессов, то она же может использоваться и для случайных величин, хотя при этом обратное не выполняется.