 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Бином Ньютона
|
|
Если 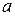 и
и 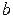 – числа, а
– числа, а 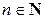 , то
, то
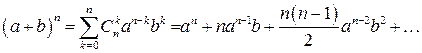
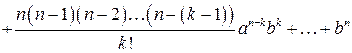 . (1)
. (1)
Следствие 1.1. 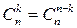 , где
, где 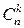 – называют биномиальными коэффициентами.
– называют биномиальными коэффициентами.
Пример 1.9. Найти сумму биномиальных коэффициентов.
Решение. Положим в (1) 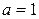 ,
, 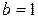 , тогда
, тогда  .
.
Сумма биномиальных коэффициентов равна 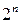 .
.
Биноминальные коэффициенты можно найти из треугольника Паскаля
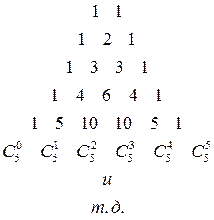
1.22. Разложите по биному:
1. 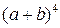 ; 2.
; 2. 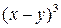 ; 3.
; 3. 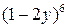 ; 4.
; 4. 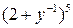 ; 5.
; 5. 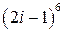 ; 6.
; 6. 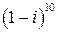 .
.
1.23. Найдите: 1) пятое; 2) 10; 3) 15; 4) 16 слагаемое в разложении 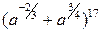 .
.
1.24. Докажите, что
1) 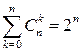 ;
;
2) Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах.
1.25. Пользуясь формулой Муавра и биномом Ньютона, выразить через степени 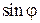 и
и 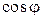 следующие функции кратных углов:
следующие функции кратных углов:
1) 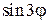 ; 2)
; 2) 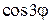 ; 3)
; 3) 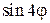 ; 4)
; 4) 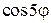 .
.
Дата публикования: 2015-09-17; Прочитано: 441 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
