Комбинаторика

Пусть дано множество (все элементы различны). Обозначим произведение 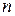натуральных чисел («эн факториал»). По определению .

Определение 1.8. Перестановкой из 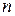элементов называется любое упорядоченное множество из этих 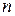элементов.

Пример 1.3. Пусть . Найти все перестановки.

Решение. . Их количество .

Теорема 1.1. Число перестановок из 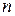элементов равно

Число перестановок обозначают . Итак, .

Пример 1.4. Сколькими способами можно разместить 5 гостей

1) в ряд;

2) за круглым столом.

Решение.

1) .

2) Зафиксируем одного гостя. Остальных упорядочим относительно выбранного .

Определение 1.9. Размещением из 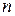элементов по элементов называются перестановки по элементов, взятые из множества в 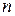элементов. Обозначение числа размещений .

Теорема 1.2. Число размещений .

Пример 1.5. Найти все размещения по 2 элемента из множества .

Решение. . Их количество

Пример 1.6. Сколько четырёхбуквенных слов можно составить из 7 различных букв.

Решение.

Определение 1.10. Сочетанием из 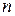элементов по элементов называется любое неупорядоченное подмножество из элементов множества в 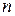элементов.

Число сочетаний обозначается .

Пример 1.7. Дано . Найти все сочетания по 2 элемента.

Решение. ; . Порядок элементов нам не важен.

Теорема 1.3. Число сочетаний

Пример 1.8. Сколькими способами можно выбрать 3 дежурных из группы в 30 человек?

Решение. .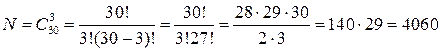

1.14. Найдите: 1) 0!; 2) 5!; 3) 7!; 4) ;5) .

1.15. Сократите дробь: 1) ; 2) .

1.16. Решить уравнение: .

1.17. Найдите: 1) 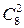; 2) ; 3) ; 4) ; 5) .

1.18. Докажите, что .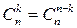

1.19. Докажите равенство: 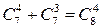; 2. .

1.20. Докажите, что .

1.21. В некотором царстве все люди отличаются набором зубов. Каково население этого царства?