 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Формулы Муавра
|
|
 ;
;
 , где
, где  .
.
1.1. Выполнить действия, ответ записать в алгебраической форме:
1.  . .
| 2.  . .
|
3.  . .
| 4.  . .
|
5.  . .
| 6. 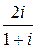 . .
|
7.  . .
| 8.  . .
|
9.  . .
| 10.  . .
|
11. 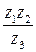 , , 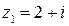 , ,  , ,  . .
| 12.  , ,  , ,  , ,  . .
|
1.2. Решить уравнения и проверить подстановкой корней в уравнение:
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
6.  .
.
1.3. Представить в тригонометрической форме комплексные числа:
| 1. 1. | 8. –1. | 15.  . .
|
| 2. 5. | 9. 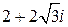 . .
| 16.  . .
|
| 3. –2. | 10.  . .
| 17.  . .
|
4.  . .
| 11.  . .
| 18. 
|
5. 
| 12.  . .
| 19.  . .
|
6.  . .
| 13.  . .
| 20.  . .
|
7.  . .
| 14.  . .
| 21.  . .
|
1.4. Вычислить:
1.  . .
| 4.  . .
| 7.  . .
|
2.  . .
| 5. 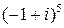 . .
| 8.  . .
|
3.  . .
| 6.  . .
| 9.  . .
|
1.5. Найти все значения корней:
1.  . .
| 4.  . .
| 7.  . .
|
2. 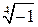 . .
| 5.  . .
| 8.  . .
|
3.  . .
| 6. 
| 9.  . .
|
1.6. 1) Доказать, что сумма и произведение взаимно сопряженных комплексных чисел являются действительными числами.
2) Доказать равенства:
1.  .
.
2.  .
.
3. 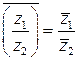 ..
..
4.  .
.
1.7. Найти формулы для вычисления степеней числа i.
1.8. Найдите: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
1.9. Как расположены на комплексной плоскости: 1) сопряженные числа; 2) противоположные числа; 3) корни n -ой степени?
1.10 Решить уравнения:
1.  . .
| 3.  . .
| 5.  . .
|
2. 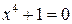 . .
| 4.  . .
|
1.11. Решить уравнения:
1.  ;
;
2.  ;
;
3.  .
.
1.12. Где находится точка z комплексной плоскости, если точка 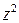 принадлежит мнимой оси?
принадлежит мнимой оси?
1.13. Найти действительные корни уравнения 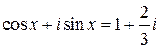 .
.
Дата публикования: 2015-09-17; Прочитано: 373 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
