Непрерывные СВ

Непрерывной СВ в широком смысле называется СВ, которая может принимать все (бесконечно много) значения из некоторого конечного или бесконечного промежутка. Если функция распределения везде непрерывна и имеет производную, СВ называется непрерывной в узком смысле.

Пример:

1. Координаты точки попадания при выстреле.

2. Время опоздания поезда.

3. Время безотказной работы лампы.

3.5.1. Формы представления закона распределения НСВ

Ряд распределения, многоугольник распределения и формула не используются в качестве закона распределения НСВ.

Функция распределения НСВ , есть непрерывная, кусочно-дифференцируема функция с непрерывной производной.

График функции распределения НСВ , которая принимает все возможные значения на интервале .

Из свойства 2 функции распределения вытекает важное следствие для НСВ: вероятность того, что НСВ примет одно определенное значение равна 0. И тогда

Таким образом, не представляет интереса говорить о вероятности того, что НСВ примет одно определенное значение, но имеет смысл рассматривать вероятность попадания ее в интервал, пусть даже сколь угодно малой.

При этом надо понимать, что не означает, что событие невозможно. В результате испытания НСВ обязательно примет одно из возможных значений, в том числе и .

Плотность вероятностей (плотность распределения вероятностей, плотность) НСВ - функция, определяемая как первая производная функции распределения

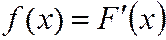(3.12)

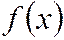Из определения следует, что - есть первообразная и выражается через 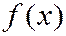формулой.

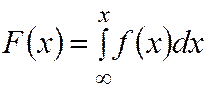(3.13)

Геометрически есть площадь кривой распределения, лежащая левее точки .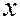

График 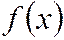называется кривой распределения.

Размерность 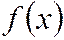обратна размерности СВ (это не вероятность).

Свойства :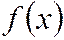

1. 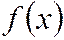неотрицательная функция, т.е.

2.Несобственный интеграл от 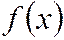на интервале равен 1.

(3.14)

Это так называемое условие нормировки плотности распределения.

Если все возможные значения НСВ принадлежат интервалу 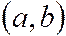, то

(3.15)

3. Вероятность того, что НСВ примет значение из интервала 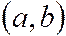равна определенному интегралу от 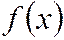, взятому на интервале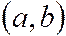

(3.16)

Геометрически это означает, что есть площадь под кривой распределения, ограниченная линиями и слева и справа соответственно и осью абсцисс внизу.

Величина для НСВ называется элементом вероятности и приближенно равна вероятности попадания СВ на элементарный отрезок , примыкающий к точке .

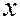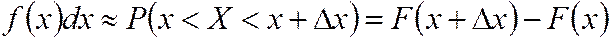(3.17)

Пример. Для НСВ , плотность распределения которой имеет вид

1) Определить коэффициент ;

2) Построить кривую распределения;

3) Найти и построить её график;

4) Вычислить

Решение:

1. По (3.14)

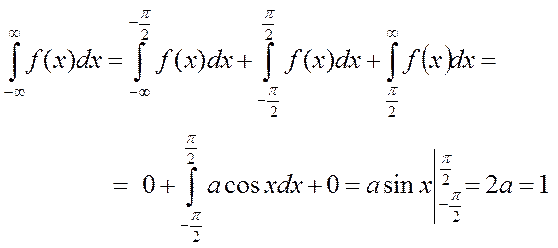
2. Кривая распределения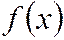

3. По (3.13)

При

При

При

График функции

4. Согласно второго свойства