Поняття про термодинамічну систему, термодинамічний процес. Ідеальний та реальні гази. Закони ідеального газу. Рівняння стану ідеального газу

План

1 Поняття про термодинамічну систему, термодинамічний процес.

2 Ідеальний та реальні гази. Закони ідеального газу.

3 Рівняння стану ідеального газу. Газова постійна та універсальна газова постійна.

1 Термодинамічна система – сукупність матеріальних тіл і полів, які взаємодіють між собою і зовнішнім середовищем, тобто обмінюються енергією і речовиною.

Термодинамічна система, яка не обмінюється з зовнішнім середовищем ні енер-гією, ні речовиною, називається ізольованою або замкненою.

Якщо з плином часу параметри стану термодинамічної системи при постійних зовнішніх умовах не змінюються, то вона знаходиться в рівноважному стані.

Всяка зміна параметрів стану робочого тіла називається термодинамічним про-цесом, або скорочено процесом. Кожен процес здійснюється при тепловій і механіч-ній взаємодії робочого тіла з зовнішнім навколишнім середовищем, при цьому стан останнього також змінюється.

Термодинамічний процес, який складається з безперервного ряду рівноважних станів, називається рівноважним.

При вивченні термодинамічних процесів використовується їх графічне зобра-ження в різних координатних системах, зокрема, в системі координат 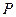і , яка нази-вається діаграмою. По осі ординат відкладаються абсолютні тиски, по осі абсцис – питомі об’єми газу. При заданих 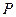і рівноважний стан зображується точкою, а рівноважний процес – в загальному випадку кривою лінією.

Зобразимо в діаграмі довільний рівноважний процес лінією 1–2 (рису-

нок 1.3). З графіку видно, що при переході газу з початкового стану 1 в кінцевий 2 відбувається зниження тиску і збільшення питомого об’єму. Це є процесом розши-рення газу, який вважається прямим процесом. Зворотний процес -це процес стиснення газу, коли він із стану 2 переходить в початковий 1; при цьому відбувається зменшення питомого об’єму і збільшення тиску.

Характерною властивістю рівноважних про-

цесів є їхня оборотність. Це означає, що якщо

при розширенні зі стану 1 газ проходить через

проміжні рівноважні стани а, в, с, f, m (рису-

нок 1.3), то при зворотному процесі стиснення зі

стану 2 газ пройде через ті ж стани, але в зворот-

ній послідовності m, f, c, в, а і повернеться в

початковий стан 1.

У зв’язку з цим рівноважні процеси назива-

ються оборотними процесами.

Рисунок 1.3 – Зображення оборотного процесу

В результаті протікання спочатку прямого, а потім зворотного рівноважних процесів в термодинамічній системі „робоче тіло – довкілля” ніяких змін не відбудеть-

ся.

Рівноважні оборотні процеси є ідеальними, які в першу чергу розглядаються ТД. Всі реальні процеси протікають з великою швидкістю і при наявності кінцевої різниці температур і тисків між газом та зовнішнім середовищем. Тому ці процеси будуть нерівноважними і, отже, необоротними. Вивчати реальні необоротні процеси важко, і тому ТД вивчає тільки теоретичні оборотні процеси. Це виправдовується також і тим, що на практиці відхилення реальних процесів від ідеальних незначне і не приймається до уваги. При великих відхиленнях перехід від ідеальних процесів до реальних здійснюється шляхом введення поправочних коефіцієнтів, отриманих у дослідах.

2 Реальні гази складаються з атомів і молекул, які знаходяться в безперервному хаотичному русі. Між молекулами діють сили притягання і відштовхування, об’єм часток має кінцеву величину. Одначе часто гази знаходяться в такому стані, коли сили взаємодії незначні, як й об’єм молекул, тому і тим, і іншим можна знехтувати.

Газ, у котрого відсутні сили взаємодії між молекулами, а їхній об’єм у порівнянні з повним об’ємом, який займає газ, дорівнює нулю, називається ідеальним.

Введення поняття „ідеальний газ” має велике значення, бо дозволяє достатньо просто одержати аналітичні залежності, які описують його поведінку. Ці залежності в ряді випадків можуть бути застосовані до опису поведінки реальних газів. Такі гази, як кисень, водень, азот, повітря при відносно низьких тисках і високих температурах за своїми властивостями стають схожими до властивостей ідеального газу. Тому при термодинамічних дослідженнях процесів, які протікають в цих газах, використовують закони і рівняння стану ідеального газу. Введення поняття ідеального газу полегшило завдання термодинамічних досліджень, дозволило отримати прості математичні рівняння для підрахунку різних фізичних величин, які характеризують зміну стану робочого тіла.

Закон Бойля – Маріота. Якщо постійна кількість газу (наприклад, 1 кг) при постійній температурі () буде переходити з одного стану з параметрами , в інший - з параметрами , , то його абсолютний тиск буде змінюватися зворотно пропорційно питомому об’єму, тобто

або (1.11,1.12)

При постійній температурі добуток абсолютного тиску на питомий об’єм даної маси газу є величина постійна.

Закон Гей – Люсака. Якщо нагрівати або охолоджувати постійну кількість газу (наприклад, 1 кг) при постійному тиску (), то питомий об’єм газу змі-нюється прямо пропорційно його абсолютній температурі, тобто

(1.13)

Закон Авогадро. В рівних об’ємах різних газів міститься однакова кількість молекул, якщо ці гази будуть мати однакові абсолютні тиски і температури.

З закону Авогадро витікає, що при однакових абсолютних температурах і тисках щільність газів пропорційна їх молекулярним масам 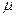, тобто

(1.14)

Через те що, , , звідки 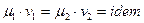(1.15)

Кількість газів в грамах, яка дорівнює числу одиниць молекулярної маси, нази-вається молем. Моль визначається як кількість речовини, яка містить стільки ж моле-кул, скільки міститься атомів в вуглецю-12 масою 0,012 кг. Один кіломоль дорівнює 1000 молей і позначається 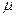, . Добуток є об’ємом кіломолю газу , .

При нормальних фізичних умовах (, ) об’єм одного кіломолю будь-якого газу дорівнює 22,4 , тому

. (1.16)

Звідси щільність і питомий об’єм будь – якого газу при нормальних фізичних умовах визначаються з простих співвідношень:

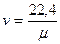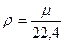, . (1.17,1.18)

3 Для рівноважного стану газу існує однозначна залежність між його основними пара-метрами 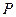, v і Т, яка виражається аналітичним рівнянням, що називається рівнянням стану. Воно було отримано Клапейроном в 1834 р. шляхом використання дослідних законів Бойля – Маріота і Гей – Люсака і має вигляд:

для 1 кг , (1.19)

для довільної маси газу , (1.20)

для 1 кмоля газу , (1.21)

Останнє рівняння називають рівнянням Менделєєва – Клапейрона, а величину

- універсальною газовою постійною, бо для всіх газів і в певному стані вона має одне й те ж значення. Визначити це значення можна по рівнянню (1.21), якщо параметри стану 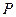і Т взяти при нормальних умовах ( =101325 Па, Т= -273,15 )

(1.22)

Величина () є індивідуальною характеристикою даної речовини і назива-ється газовою постійною. Визначається виразом

. (1.23)