 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Расчет интерференционной картины от двух когерентных источников
|
|
Два когерентных источника можно получить, например, методом Юнга. Рассчитать интерференционную картину - это значит предсказать, в какой точке экрана наблюдения будет максимум, а в какой минимум интенсивности (рис. 3.9).

Рис. 3.9
На рис. 3.9 приняты следующие обозначения:
S1 и S2 - когерентные источники;
d - расстояние между когерентными источниками;
L - расстояние от источников до экрана наблюдения;
Δ x - разность хода, Δ x = S2 M - S1 M;
Δ y - ширина интерференционной полосы;
ym - координата темной или светлой интерференционной полосы с номером m; 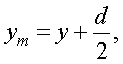 где y - координата от центра картины. Учтем, что уm >>
где y - координата от центра картины. Учтем, что уm >> 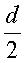 , тогда уm ≈ y.
, тогда уm ≈ y.
Кривая с максимумами и минимумами представляет собой распределение интенсивности вдоль экрана наблюдения.
Для того чтобы рассчитать интерференционную картину, рассмотрим два подобных треугольника: 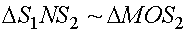 .
.
Из  найдем синус угла α:
найдем синус угла α: 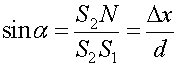 ; из
; из 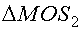 найдем тангенс угла α
найдем тангенс угла α  .
.
Так как угол α мал, то  и
и  . Тогда координата интерференционной полосы с номером m равна
. Тогда координата интерференционной полосы с номером m равна
 .
.
Для светлых полос выполняется условие максимума. С учетом (3.37) координата светлой полосы определяется по формуле:

Аналогично координата темной полосы с номером m с учетом (3.38) равна:

Шириной интерференционной полосы называется расстояние между соседними максимумами или расстояние между соседними минимумами (рис. 3.8):

Рассчитаем ширину интерференционной полосы для светлых полос:

Формула 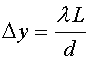 (3.39) показывает, что для того, чтобы интерференционная картина была отчетливой, необходимо соблюдение условия d << L. Эту формулу можно использовать для того, чтобы определить длину волны света
(3.39) показывает, что для того, чтобы интерференционная картина была отчетливой, необходимо соблюдение условия d << L. Эту формулу можно использовать для того, чтобы определить длину волны света

Именно таким способом впервые были определены длины волн для световых лучей разного цвета.
Формула (3.40) является рабочей в лабораторной работе "Изучение интерференции света".
Дата публикования: 2015-09-17; Прочитано: 3247 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
